No, Seriously... I Need Your Help

Alright, my head is about to explode.  For the next two days I'll be sitting here in a room all alone trying to figure out how the heck we are supposed to bridge this gap. I have all the tools ready to go(computers, legal pads, pens, state framework,etc.). And all of a sudden it hits me.  The rules of math have come about because they were necessary.  For example, Natural numbers work until you try to subtract.  Then you have to have integers. Integers are fine until you divide, which leads to Rational numbers.  The Rational numbers  break down when you try to find the side length of a square with an area of 15.  Take the kids on this tour and we get to say: "Okay class, we have just discovered the Real Number system."

We have exponents and scientific notation because it get really tedious to multiply (5,000,000,000)(8,000,000) by hand.  We introduce the symbols and variables because we don't want to have to work out every single case for every single situation. We generalize because mathematicians are inherently lazy.  We truly find the shortest distance between two points. Kids are inherently lazy; they know the shortest distance between homework and their XBox.  Hey, we have someting in common.  How do we expolit that commonality in order to have kids "discover" algebra for themselves? How do we scaffold our entire curriculum, so that kids move from the Natural Numbers to Projectile Motion in such a way that they actually see how there is a need for it?

I realize that I am probably not saying anything you all haven't already discovered for yourselves.  But, before I go and reinvent this wheel, I would like to know what you have all been doing to get this Algebra bus rollin'.

Dear Dan,

You are really starting to make me angry.  I was content to just do my job, help as many kids as I could, do some extra stuff to help them make it connect to their reality.  And then at 4:00pm shut it down, go home, kiss my wife, play with the kids, have a nice dinner, watch a little TV and go to bed.  But no!  You just had to start in with all this "using pictures to help kids learn math" stuff.  You couldn't leave well enough alone.  When I couldn't get Graphing Stories to work, you couldn't just say "sorry dude, I am not sure why those chapters won't play.  Better luck next time"... no you had to send me a copy and not even take the reimbursement I offered.  Who do you think you are?

Man I can't even go to Target with my family without trying to take a picture of something.  You know how disruptive that is?  You know how hard it is to hold the baby, push the cart and snap a pic at the same time?  I am looking into having an extra arm grafted onto my torso.  You think my insurance will cover that?  Nooooo! And it is all because of YOU! 

The worst part is that I have these video cameras lying around my classroom and a blue screen in the library so I had to skip lunch the other day and take some footage that has resulted in some stills like these:

 

 

 I mean, look at that.  How can they not see that the ball is accelerating as it falls?  I don't want that.  I want them to depend on me to tell them that gravity is an acceleration.

[caption id="attachment_134" align="aligncenter" width="300" caption="I'm not mad at you for this one, I actually think it's pretty cool. "]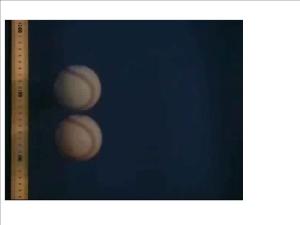[/caption]

What's even worse, is I have all this raw video footage and I have no friggin' idea what to do with it. What am I supposed to do, have students graph the height of the ball vs. time and realize that there are some relationships that aren't linear?

My students are even getting into the taping.  They look so cute  and happy throwing the ball back and forth, but little do they know that one day this concept of math actually helping them  to interpret the world around them can consume them.  What's next?  Are we going to start treating mathematics like a humanity and sit around discussing it as if it were a piece of literature or work or art?  Don't you know that math is only supposed to be important  8:20-2:55 in Room 405 from September to June?  Don't you know that math is supposed to be a set of rules that we force our kids to memorize until April 22 and then they aren't supposed to think about it again?  Get with the program, will ya?

And no textbook?  C'mon, man!  What are you thinking?  Those things were all written by people who really care about making math matter to our children. Don't you know that the more a student sits in front of a textbook, the more they learn?  I saw some research done by an independent agency Houghton, McGraw, Holt and Littell that says students can actually teach themselves with these things.

In closing, you have got it all wrong.  Kids want to have subjects forced upon them.  They want to be told the rules, they want to mindlessly copy exactly what the teacher says and does and they especially want to ask questions like, "I don't get it." 

Inquiry?  Yeah, right!

Sincerely,

David

p.s. Can I make a cameo in Graphing Stories vol. 2?

p.p.s Can you all help me package this up into a series of lessons?

The Never Ending Question

Teacher: So what is the value of f(x) if x =3?

Student: Does f(x) mean f times x?

Teacher: No, no, no...f(x) is a function of x. 

Student: Oh, it is a function of x?

Teacher: Right.

Student: Oh, okay,  I think I get it.  So we can plug in a number for x and find out what f equals. 

Teacher:  Yeah, that's pretty close.  Do you have another question? 

Student: So, then is f like the slope of the line?

Teacher: *slaps forehead*  Uncle!

Student: Well you said it is a function of x and of means to multiply.

Alright, so that didn't just happen in my class.  But similar dialogues do take place right around the time I first introduce things like f(x) or sin(x).  Kids always think that means that we are multiplying something by x.  We usually end up discussing how often times functions need to have names like f(x) or g(x) so you can tell them apart.  We don't spend too much time on function notation in middle school, but when it comes up, I would like a better way to explain it.

Don't act like that hasn't happened to you.  

So how do you explain it?

Sincerely, Markus Hohenwarter

Every day at 5:00 pm I receive an email from Markus Hohenwarter.  It isn't a "hey how are you doing?" kind of email, this one is all business.  Actually it isn't even a personal email, it is one of those mass emails that often ends up in the spam box.  But more times than not, this spam is worth reading. 

Markus Hohenwarter is the creator of GeoGebra which has to be one of my top three classroom tools.  The email is generated by the Geogebra upload manager and lists all of the different GeoGebra files (both .html and .ggb) that have been uploaded to the bank during the previous day.   Many of the dynamic .html worksheets are ready for classroom use and author attribution is at the bottom of the page.  However, if you like the concept of the worksheet but would like to use your own questions, you can download the .ggb file and learn how the sheet was created by viewing the construction protocol. 

The only downside to the upload manager is that the uploads aren't tagged, so you have to do bit of hunting to find someting worth while.  Regardless, this is yet another reason to love GeoGebra!

Bridging the Gap

This one goes out to all the algebra teachers; especially those in middle school.  Anyone notice that kids "get it" in 7th grade and then act like they have never seen a variable once they hit algebra? Or am I the only one?  We had nearly 70% of our 7th graders proficient and above on last year's CST's, but only 40% of our algebra students were proficient.  If you take the advanced classes out of the mix, it is more like 60% to 30%.  I know, I know, you can't base what a kid knows solely on a standardized test.  But, those numbers are pretty indicative of how the kids actually do in class.  Some will say that algebra is just too abstract for most 8th grade kids.  I don't know if I buy that, especially when I read articles like this.  

I am going to have some release time once testing is over in order to adjust our pacing guides and I would like to be able to develop some lesson ideas to help our teachers bridge the gap between number sense and algebraic thinking.  Maybe some of you have already tackled this.  I would love to hear what you have done.  How have you sequenced your 7th grade curriculum and how have you helped move your students from numeric fluency to algebraic proficiency?  I figure if I am going to lock myself in a room and try to hash this out, you may as well be there with me!

Can I Get In Trouble For This?

Testing started today. I have done everything within my power to make my classroom as non-mathy as possible.  No work on the boards.  All procedure posters covered.  I even attempted to remove the letters A,B,C,D,F,G,H,J from any text on my walls.  However, this one slipped by:



Uh oh!  I am sure this is one of the answers to one of the problems.  I hope the students don't see it.

Confessions of a 13 Year Veteran

Ok, I admit it.  My lesson planning skills suck!  It just hit me the other day. I am reading all your blogs and seeing all the cool things you are doing in your classrooms, and all I can ask myself is, "Why don't I think of stuff like that?" 

 I think I know why.  I cut my teeth on CPM (another post on CPM coming soon) and all of my lessons were pre packaged.  All I needed to learn was to ask good questions and get out of the way.  That suited my style very well.  By the time NCLB came around and we dropped CPM, my school was already going lock step with pacing guides and common assessments.  Neither one of these approaches allowed for much innovation nor did they require a bunch of thought.  It didn't help that I became the varsity baseball coach in my first full year of teaching and spent way more time planning practice than I did lessons.  The real problem was that I didn't really know how much I had bitten off until recently. 

Now that I am teaching middle school math as the high school guy brought in to handle all the GATE kids, I am not only responsible for my own classes but for setting a tone and pace for an entire department.  I feel more accountability now than ever before.  It has been in these last three years that I have really started to ask reflective questions regarding not only my practice, but good practice in general.  I also have access to tools that I didn't even know existed when I was at the high school. 

So here is a snapshot of where my lessons were compared to where they are.  Feel free to take your shots and help me make this better.  This lesson is stolen  borrowed adapted from a lesson in the April 2009 issue of Mathematics Teaching in the Middle School. 

What I would have done before:

I don't know if I would have even bothered to re type the lesson, I may have just photo copied it and given it like this:



I would have passed out this handout and told the students to represent each savings plan as a: graph, input/output table, algebraic expression and verbal expression.  My students would have muddled through it and most would have just jumped through another hoop. 

What I did today:

I toggled between these four slides and asked students to pick out what information they thought was important.  It was interesting that some students felt it necessary to try to copy the information while the rest of the class was willing to observe and jot down what they thought was essential info.

 



Questions students came up with:

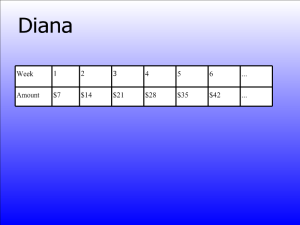
• Does the chart represent the amount of money Diana makes each week or the total she has saved?


• Will she continue to save at this rate? "Yeah, look at the "dot, dot, dot."

Teacher: "What can you tell me about Yoni?"

Class: "She has $300."

Teacher: "How much will she have in 3 weeks? 2 years? 100 years?

Class: "$300. $300. $300."



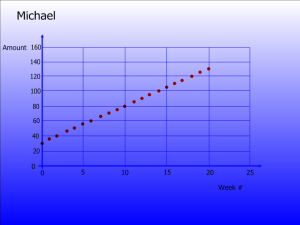
A few students were quick to point out that we only needed to focus on two or three key points in order to make a generalization of Michael's situation.  They immediately zoomed in on (0, 30) and (10, 80).  However, I did have one group who decided to focus on the last point (20, 130). They decided that Michael averaged $6.50 per week.  But when they were asked if their trend would continue, they quickly realized that they had failed to consider the original amount of Michael's savings.

Chandler, one of my 7th graders decided to ask, "Does x represent weeks?"  Beautiful, that info was on the next slide. 

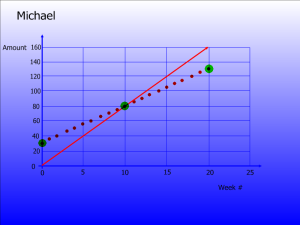
The question of the day had to come from Paul: "So, if the only point we know for sure in Michael's graph is (30, 80) wouldn't he have more money if he actually started at (0,0)?  In his mind he was seeing this...



...which led to an interesting discussion on how slope represents the amount of money saved per week. 

My students are starting to catch on to how things work in my class because as soon as these slides came up:





I asked, "What is my next question?" To which they all responded:



Once they had made the decision on which represenation they prefered, I had them represent the other three savings plans the same way.

At first the justifications for "why" one representation was preferred over another were weak at best, lazy and unthoughtful at worst:

• An input/output table is more organized.


• It's easier to see the data.


• I like it better because it is better and less worse than the others.

Okay, that last one was mine, but you get the point.  Being the father of four boys, I can smell an "alright get off my back, already" answer a mile away, I continued to prod.  Eventually we had answers like this:

• I prefer the chart because it is easier to see which numbers go together; on the graph, you have to work a little more to see which numbers are related.


• I prefer the graph because I can actually see how the different points relate.  The slope helps me see how fast someone is saving.


• I prefer the verbal expression because it helps me understand the overall situation better.

We eventually got to the discussion on "Who has the most money right now?"

Hands fly upright around the same time I hear: "Yoni! Danny!" 

Then Adrian pipes up, "When is now?"

Gotta love that kid!

Semester Project

Because my district is in program improvement, there has been a huge push to do things "one standard at a time."  Not a bad idea since the standards (for algebra anyway) are pretty solid.  The problem lies in the fact that there is a tendency to simply teach the skills and neglect the conceptual development as well as problem solving aspect to algebra.  So I decided to call a buddy of mine who happens to be a farmer and here is a project I came up with.  I created an answer key using GeoGebra that allows for quick checking of student progress.  Feedback request: I would really like some input on this one.  I know that I would like to use it again next year, but I know it needs some work.

What Did They Do With It?

So I took a stab at letting my kids have a go at Dan's last installment. And to say I was pleased is the understatement of the year.  The first obvious question was "will it go in the can?" But, since we have finished going over parabolas, kids started asking questions like:

• How high was the ball at its highest point?


• How far did it travel?


• What was its velocity?


• How long was the ball in the air?

The question that really opened one of those "teachable moments" was in regards to velocity.  To this point we have only covered vertical motion.  These kids understand how to model a falling object as well as an object with an initial velocity other than 0.  This led to an interesting discussion.  Does the "falling object" or "thrown object" apply here?  And that is when Lio hit the nail right on the head. 

He pipes up with, "Hey Mr. Cox, if we shoot a gun horizontally and drop a bullet from the same height instantaneously, they both hit the ground at the same time right?"

"Yup."

"So does the fact that it is travelling horizontally have anything to do with how fast it falls?"

"Nope."

"So can we use the stuff we know about falling objects here?"

"Yup."

"But we need heights." 

"Well I guess we are done here."

That is when Seth walks over to the trash can and measures how tall it is.  All these trash cans have to be the same, right?



And the rest is history.  The kids opened up the computers, dragged the images into the SmartNotebook software and here is what Group 1 came up with: 

Here is where it gets really cool.  My other Seth asks if we can find the actual distance the ball travels along the parabola.  He thinks that if we can measure the distance between the balls, then we could get a series of straight lines.  He comes to the conclusion that the closer the balls are to each other, the more accurate our approximation is. 

Wait till he gets a load of Calculus.  Did I mention he is 13?

Professional Development

I have to confess.  I am a bit upset.  Why is it that I have been teaching for 13 years and have yet to encounter a professional development session that wasn't an utter waste of my time?  Why is it that the majority of  educational conversations focus on what kids can't do and how we can't change the way we do business because, well, "that's just how we do it here?"  If Jack Johnson were a teacher he'd sing "Where'd all the good conversations go?"  Why is it that when someone sets foot in another teacher's classroom it is assumed that the visitor is looked at as an intruder?  Why did it take me so long to find teachers who are asking really tough questions-really good questions?  Why wasn't I looking? Why wasn't I asking them myself?

I have tried to teach my students that the answer isn't the point.  It is all about the question.  The beauty of it is that the more questions I find answers to, the more questions I have.  A few months ago I stumbled across Classroom 2.0 and asked a question about dealing with gifted kids.  It wasn't long before I was in the middle of a conversation with Nancy Bosch about how to deal with gifted students that she says, "Hey there is a guy named Dan who is asking some pretty good questions.  You are both math guys; check him out."  So I do and realize that we are practically neighbors. (Okay, we both live in CA but Nancy is in Kansas.) So now I realize that all of those good conversations? All the good questions? Yeah, they are right here.  Right Now!  And I don't have to sit in a 3 hour meeting to join them. 

So again I ask:  Why have I had more professional development in the past 4 months than in the previous 13 years?  Was I not listening?  Or was no one showing me where to listen?

The Easter Egg Hunt

Every nine weeks my district gives benchmark exams covering approximately one-third of the standards that have been deemed "essential."  Many teachers feel the need to do a bunch of last minute cramming and do intensive review.  For the most part, I see the benchmark as a speedbump; one of those things that I have to do.  I mean, I we already have department CFAs (common formative assessments) that we use to re-direct our instruction, so I pretty much already know where my kids stand.  So for the last benchmark of the year, I decided to change up the review.

I made up a practice test covering the standards that would be assessed, uploaded it to voicethread and had students sign up to create a mathcast for specific problems.  However, this time they were looking for a fastball up and in and I gave them a change away. I asked a few students to do the problems incorrectly (of course, first they had to demonstrate to me that they could do the problem right.) Once everyone had added their comments to the Voicethread, I assigned the Easter Egg Hunt--Which ones are wrong and why? I think I really like this activity. Students not only have to work out each problem themselves, but they have to view another's work critically. I would love to hear what you think.

I'm Jumping In

Alright, here it goes.  I have been browsing the world of edublogs for a while and have been impressed with the quality of dialogue.  The sad thing is that I think I have enjoyed more professional development from these online discussions than I have from countless inservices, staff meetings and trainings.  So, I figure it is time to join the conversation.