About this time last year, I didn't know much about blogs, Twitter or PLN's. I did, however, have questions about why we do what we do and how to make it matter. This blog was born because there are a lot of great teachers having great conversations and I thought 14 years of going it alone was enough. It continues to boggle my mind that many of you have a better idea of what takes place in my classroom than many of the teachers in my own school; it matters to you what is happening in classrooms of others. I hope that in the next year, the questions asked here will be more honest and continue to challenge.
I am humbled and honored that Sam and Kate found this blog worthy of a Best New Blog nomination. If you feel so inclined, you may cast your vote here.
Monday, December 14, 2009
Thursday, December 10, 2009
Triangle Centers Lab
The other day I made up a triangle centers lab for my 8th graders.
Here is how it went:
Day 0: Homework for tonight is to make a triangle larger than your hand out of some material heavier than paper. Cardstock or cardboard are ideal.
Day 1: Open GeoGebra and get to work. Kids got after it. Some slowed themselves down by not reading directions very well. The nice thing about GeoGebra is that it's easy to erase.
Day 2: Most finished the lab and went onto extension activity. Those who didn't finish had a difficult time managing time. They could do the work, but staying focused was the issue.
Extension: Now that you know how to find the circumcenter and incenter, construct an inscribed and circumscribed circle using only compass and straight edge. These students haven't done anything with a compass, so I offered a 6th point (assignment was worth 5) for those who could figure out how to do the constructions on their own. If they chose to look up the "how to" of constructions, they then would have to prove that the method of angle bisecting works.
David came up with his own extension. He asked, "why does the centroid allow you to balance the triangle?"
"Nice question. Now go away and come back with an answer." He's figured out that the three medians divide the triangles into six smaller triangles with equal area and that would account for equal weight distribution from the centroid. He can see it in GeoGebra, but is working on a formal proof. Brandon tried to backdoor me with a proof by contradiction, "well the six triangles have to have equivalent areas because if they weren't, the large triangle wouldn't balance."
Don't try to beat me at my own game, son.
Chris' reflection: "Hey Mr. Cox, you just kinda gave us a test without giving us instructions."
"Yeeeeaah kinda, huh?
For Next Time: Stamp each page after students have demonstrated the correct constructions. Then allow them to go to the next page. Take a little more time discussing the difference between "drawing" and "constructing."
Here is how it went:
Day 0: Homework for tonight is to make a triangle larger than your hand out of some material heavier than paper. Cardstock or cardboard are ideal.
Day 1: Open GeoGebra and get to work. Kids got after it. Some slowed themselves down by not reading directions very well. The nice thing about GeoGebra is that it's easy to erase.
Day 2: Most finished the lab and went onto extension activity. Those who didn't finish had a difficult time managing time. They could do the work, but staying focused was the issue.
Extension: Now that you know how to find the circumcenter and incenter, construct an inscribed and circumscribed circle using only compass and straight edge. These students haven't done anything with a compass, so I offered a 6th point (assignment was worth 5) for those who could figure out how to do the constructions on their own. If they chose to look up the "how to" of constructions, they then would have to prove that the method of angle bisecting works.
David came up with his own extension. He asked, "why does the centroid allow you to balance the triangle?"
"Nice question. Now go away and come back with an answer." He's figured out that the three medians divide the triangles into six smaller triangles with equal area and that would account for equal weight distribution from the centroid. He can see it in GeoGebra, but is working on a formal proof. Brandon tried to backdoor me with a proof by contradiction, "well the six triangles have to have equivalent areas because if they weren't, the large triangle wouldn't balance."
Don't try to beat me at my own game, son.
Chris' reflection: "Hey Mr. Cox, you just kinda gave us a test without giving us instructions."
"Yeeeeaah kinda, huh?
For Next Time: Stamp each page after students have demonstrated the correct constructions. Then allow them to go to the next page. Take a little more time discussing the difference between "drawing" and "constructing."
Friday, December 4, 2009
To Wiki or Not to Wiki
I know, I know:
"Using a tool for it's own sake is bad pedagogy."
"Have an objective and then find the tool that will help you best meet that objective."
"If your favorite tool is a hammer, everything looks like a nail."
Blah, blah, blah.
What if you didn't know if your objective was even possible until you tried out the tool? Then what?
I completely understand Kate's frustration when it comes to the speed bumps caused when we try to rely on certain tools. But what about just making the tool available and allowing kids to come and go as they see fit? Why can't we do that? Does everything have to have a lesson plan attached to it?
I originally created this wiki just because I could. I let kids take some class time to familiarize themselves with how to use it--in fact, we learned how to use it together. But the space has taken on a life of it's own. I have kids who are now in high school coming back to access the resources they created last year.
That's a good thing, no?
"Using a tool for it's own sake is bad pedagogy."
"Have an objective and then find the tool that will help you best meet that objective."
"If your favorite tool is a hammer, everything looks like a nail."
Blah, blah, blah.
What if you didn't know if your objective was even possible until you tried out the tool? Then what?
I completely understand Kate's frustration when it comes to the speed bumps caused when we try to rely on certain tools. But what about just making the tool available and allowing kids to come and go as they see fit? Why can't we do that? Does everything have to have a lesson plan attached to it?
I originally created this wiki just because I could. I let kids take some class time to familiarize themselves with how to use it--in fact, we learned how to use it together. But the space has taken on a life of it's own. I have kids who are now in high school coming back to access the resources they created last year.
That's a good thing, no?
Speaking Mathanese
Kids butcher the Mathanese language. I'm just sayin'. We have all these kids who speak text just fine. It seems to me that Mathanese should be right up their alley. All we are doing is taking a bunch of words and converting it to symbols. Should be easy, right? Not so much.
I find that kids have a tough time translating algebraic expressions to English and vice versa. Am I alone?
Yeah, didn't think so.
One of the things that I have been trying to focus on this year is to convey to students the universality of the things they are learning. For example, cause/effect in language arts becomes input/output in math. Conflict resolution is the same as problem solving. Language arts has expressions and sentences, so does math. Scientific method can compare to making a conjecture in geometry, testing it out and then using inductive logic to arrive at a conclusion (read: rule).
So what happens when you tell them to translate: the product of 3 and the sum of x and 2?
You get: 3x+2, right?
Not quite.
Well I figured we needed to develop a mashup of English and Mathanese; Mathglish, if you will. Here is what we came up with:
English to Mathanese:
[caption id="attachment_458" align="aligncenter" width="500" caption="This should read: The product of 2 and the sum of the product of 4 and x and 3. "] [/caption]
[/caption]
Mathanese to English:

The key this time was to allow the mashup. I live in a rural area where the Spanish speaking population is very large. Many of my kids speak and understand Spanglish. I have never done it this way before and the kids nailed it.
How do you do it?
Update: Just did a quick check for understanding 2nd period and 26/28 kids circled the bases.
I find that kids have a tough time translating algebraic expressions to English and vice versa. Am I alone?
Yeah, didn't think so.
One of the things that I have been trying to focus on this year is to convey to students the universality of the things they are learning. For example, cause/effect in language arts becomes input/output in math. Conflict resolution is the same as problem solving. Language arts has expressions and sentences, so does math. Scientific method can compare to making a conjecture in geometry, testing it out and then using inductive logic to arrive at a conclusion (read: rule).
So what happens when you tell them to translate: the product of 3 and the sum of x and 2?
You get: 3x+2, right?
Not quite.
Well I figured we needed to develop a mashup of English and Mathanese; Mathglish, if you will. Here is what we came up with:
English to Mathanese:
[caption id="attachment_458" align="aligncenter" width="500" caption="This should read: The product of 2 and the sum of the product of 4 and x and 3. "]
 [/caption]
[/caption]Mathanese to English:

The key this time was to allow the mashup. I live in a rural area where the Spanish speaking population is very large. Many of my kids speak and understand Spanglish. I have never done it this way before and the kids nailed it.
How do you do it?
Update: Just did a quick check for understanding 2nd period and 26/28 kids circled the bases.
Wednesday, December 2, 2009
Joining the Fray
I'm sorry, I couldn't help myself. I can't let Sean Sweeney have all the fun in class (see here and here). I do, however, have to credit Sean with giving me the push I needed to actually do this with my class. Thanks!
The Setup
I told my students that before the Fray was "The Fray", they were called The Phray and their lead singer was a math teacher. He wrote a song called "Solve to Save Your Life" but when they were signed they changed the name of the band and made some adjustments to the song on account of "math songs don't make the top 40, baby." It took some searching to find the archive of the old song, but I did it. I also told them that OneRepublic had a song called "Rationalize." We'll see if that one surfaces.
So with no further ado: The Phray performing their hit single, "Solve to Save Your Life."
If you want the lyrics.
We'll be releasing the official video soon.
Reflection: This really isn't my thing. I was debating whether or not to scrap the whole thing even though my 4 yr. old can now solve equations. The thing that really hit me was that me leaving my comfort zone allowed some of my students the freedom to do the same. I made some connections with kids where I may not have otherwise been able to. I also learned that playing guitar for 1.5 hours over 3 periods may cause tendonitis. Advil anyone?
The Setup
I told my students that before the Fray was "The Fray", they were called The Phray and their lead singer was a math teacher. He wrote a song called "Solve to Save Your Life" but when they were signed they changed the name of the band and made some adjustments to the song on account of "math songs don't make the top 40, baby." It took some searching to find the archive of the old song, but I did it. I also told them that OneRepublic had a song called "Rationalize." We'll see if that one surfaces.
So with no further ado: The Phray performing their hit single, "Solve to Save Your Life."
If you want the lyrics.
We'll be releasing the official video soon.
Reflection: This really isn't my thing. I was debating whether or not to scrap the whole thing even though my 4 yr. old can now solve equations. The thing that really hit me was that me leaving my comfort zone allowed some of my students the freedom to do the same. I made some connections with kids where I may not have otherwise been able to. I also learned that playing guitar for 1.5 hours over 3 periods may cause tendonitis. Advil anyone?
Wednesday, November 25, 2009
How They're the Same
I've kind of been off the grid lately-save following a few conversations via Twitter- due to the birth of my son. Thanks again to everyone for all the well wishes. Mommy and baby are doing great. Sleep is a precious commodity but I am blessed to be able to take a few days off to enjoy the adjustment to our little one. I always seem to compare my approach to teaching with my approach to parenting and vice versa. Here's the top 10:
10. The clientele will expose your bad habits.
9. You can read as many "how to" books as you want, but nothing prepares you for your first real life encounter.
8. They like it when you act goofy.
7. Sometimes you just have to wing it.
6. They get grumpy before lunch time.
5. They get sleepy after lunch time.
4. You're gonna lose some sleep.
3. Working at one makes you better at the other.
2. Balance is crucial.
1. If it stinks, change it.
10. The clientele will expose your bad habits.
9. You can read as many "how to" books as you want, but nothing prepares you for your first real life encounter.
8. They like it when you act goofy.
7. Sometimes you just have to wing it.
6. They get grumpy before lunch time.
5. They get sleepy after lunch time.
4. You're gonna lose some sleep.
3. Working at one makes you better at the other.
2. Balance is crucial.
1. If it stinks, change it.
Tuesday, November 10, 2009
It Could Be Worse
Man, I am horrible right now. No, not the tell-people-that-I'm-bad-so-they-tell-me-I'm-good kind of horrible. I mean really horrible. I am way behind in planning, grading and have way too many ideas and no way to implement them. Or if I do try to implement them, they're half-baked. It may have a little to do with a certain visitor we are expecting. But at the end of the day I have been feeling way scattered. It's not a good feeling but I know it'll pass. I have been doing this long enough to know better.
There, I said it! Let the healing begin.
There, I said it! Let the healing begin.
Jose Strikes Again
During the warm up today, I asked the question:
When does the absolute value of r equal r?
I liked the way the students handled themselves during the discussion so I took out my phone and recorded the following. After a little prodding, Jose jumped in. I'm thinking of changing his name to Q.E.D.
When does the absolute value of r equal r?
I liked the way the students handled themselves during the discussion so I took out my phone and recorded the following. After a little prodding, Jose jumped in. I'm thinking of changing his name to Q.E.D.
Monday, November 2, 2009
Thanks, G-Docs
For the past two years I have had a classroom Voicethread account. It has been really difficult to set up the accounts for the students, though. So much so, that I have put it on the back-burner until today. I saw that I could import multiple accounts as long as I had a Name, UserName, Email and Password in a .csv I could import.
Piece of cake. I set up a Google Form, embedded it on our wiki and had the kids fill it out. Done. Now I'm gonna eat lunch.
Piece of cake. I set up a Google Form, embedded it on our wiki and had the kids fill it out. Done. Now I'm gonna eat lunch.
Thursday, October 29, 2009
Almost Blew This One
Today, my 7th graders were dealing with a problem that eventually they will solve by setting up a system of equations. Right now, they don't have that in the tool kit, so guess-and-check would be the strategy of choice. Here is the problem and our first step:

One student was able to come up with the equation: 1.50 a + 2.00 d = 360, but another was quick to point out that there would be many different solutions, so we couldn't use it...yet. So the first guess is 20 and we recognize that the total is too high. Usually that indicates that the first guess is too high, so we normally go with a lower second guess. However, this time, Aaron pointed out that it didn't make sense to decrease the guess on advanced tickets because they are cheaper. In fact we want to increase that one. This is right about the time I almost lost my poker face:
Aaron: "So if we add to the advanced tickets our total will actually go down."
"Why?"
"Because for every $1.50 we add, we lose $2.00. So every time we change the tickets by one, we drop $.50. Since we need to drop $30, we need to sell 60 more tickets in advance."
At this point, I almost blew it. Nearly jumped right in and said something stupid like, "That's right Aaron. You guys get it?" To which they would have all nodded "uh-huh" and we would have moved on. But I caught myself, gave him the "eh, I am not sure about that" and removed myself from the conversation. So Aaron had to try to re-explain to his classmates what he was saying. I could tell that a couple of them got it, but many were still perplexed. After a couple of minutes I asked Jose if he could explain what Aaron was saying. Jose nailed it and a bunch of kids have an "a-ha" moment. Good stuff.
Later I asked Jose why he didn't speak up a little sooner. He said that he didn't figure that he needed to ask any questions because he understood it. I asked for a show of hands on how many understood after Jose's explanation and that's when about 15 hands shoot up.
We have been talking a lot in my classes about how important it is to join the conversation. Some kids still think that it's just about them. They don't realize that if they offer something to the conversation, not only do they benefit from explaining something they already understand, but there is no telling how many other kids benefit too.
Today, I think Jose gets it.

One student was able to come up with the equation: 1.50 a + 2.00 d = 360, but another was quick to point out that there would be many different solutions, so we couldn't use it...yet. So the first guess is 20 and we recognize that the total is too high. Usually that indicates that the first guess is too high, so we normally go with a lower second guess. However, this time, Aaron pointed out that it didn't make sense to decrease the guess on advanced tickets because they are cheaper. In fact we want to increase that one. This is right about the time I almost lost my poker face:
Aaron: "So if we add to the advanced tickets our total will actually go down."
"Why?"
"Because for every $1.50 we add, we lose $2.00. So every time we change the tickets by one, we drop $.50. Since we need to drop $30, we need to sell 60 more tickets in advance."
At this point, I almost blew it. Nearly jumped right in and said something stupid like, "That's right Aaron. You guys get it?" To which they would have all nodded "uh-huh" and we would have moved on. But I caught myself, gave him the "eh, I am not sure about that" and removed myself from the conversation. So Aaron had to try to re-explain to his classmates what he was saying. I could tell that a couple of them got it, but many were still perplexed. After a couple of minutes I asked Jose if he could explain what Aaron was saying. Jose nailed it and a bunch of kids have an "a-ha" moment. Good stuff.
Later I asked Jose why he didn't speak up a little sooner. He said that he didn't figure that he needed to ask any questions because he understood it. I asked for a show of hands on how many understood after Jose's explanation and that's when about 15 hands shoot up.
We have been talking a lot in my classes about how important it is to join the conversation. Some kids still think that it's just about them. They don't realize that if they offer something to the conversation, not only do they benefit from explaining something they already understand, but there is no telling how many other kids benefit too.
Today, I think Jose gets it.
Monday, October 26, 2009
Our Grading System
Standards Based Instruction
We decided a few years ago that the sequence of our texts don't really work for us. As a result, we began teaching one standard at a time. We have taken our state standards set up a sequence and pace in a way that makes sense to us. Some of the standards we have broken down into specific skills and these skills are what make up our gradebook.
Common Formative Assessment
Once we have done our initial classroom instruction, we give a common multiple choice assessment. This assessment is graded on a 1-4 rubric. A students next step is based on how well they do on the assessment which is a pretty fair cross-section of the different problems a student may be expect to do on the given standard. We determine the initial score based on the percentage of problems they get correct. 85-100% = 4, 70-84% = 3, 55-69% = 2 and below 55% = 1.
Less Than Proficient
The level of understand a student demonstrates determines what happens next. If a student scores a 1 or 2, he will do a series of activities that may include defining basic terms and demonstrating pre-requisite skills. Once finished with these activities, the student will then take the problems that were missed on the CFA and not only correct them, but explain what went wrong (verbally or in writing) and how to work the problem correctly. Students who score a 3 on the initial assessment are just required to make the necessary corrections with explanation. Once the corrections have been made, the student is then given a re-assessment and the new score replaces the old score in the gradebook.
Proficient
Although students may get 100% of the problems correct on the initial assessment, we still give them a 4. Our reasoning is that the multiple choice test doesn't allow our students to demonstrate understanding that goes beyond classroom instruction, but it does allow them to show proficient understanding. Students who demonstrate proficient understanding on the assessment are given the opportunity to turn the 4 into a 5 by choosing from two categories of activities. Examples of activities may be creating a mini lesson, peer tutoring or some other project agreed upon by teacher and student. The second activity is some sort of writing assignment that may require the student to explain the process or describe what skills a student may need in order to be successful with this standard. Once a student has completed these activities and has shown the ability to explain his work the score in the gradebook will be turned into a 5.
Strengths
At this point, I can say that the strengths of this system are:
Weaknesses
Questions
Adaptation for the Advanced Class
Because my classes are advanced, I have to adapt this system to suit my students' needs. Basically, I am using the standards as the "basic skills" for my class. I have a posted a series of mathcasts and study guides on each standard and the students are expected to view the online examples and do the problems in the study guide prior to taking the pretest. If a student scores above 90% on the initial assessment, there is no other work to be done on the standard--they receive a 5. Students who score below 90%, need to correct their errors, explain to me that they understand why they made their mistakes and how to fix them. Once I am convinced that they have truly corrected their errors, I give them a second assessment and the new score replaces the old one.
My reason for allowing students to earn a 5 right off the bat is that 90% of our classwork is problem solving that uses the standards as the jumping off point. Students in my 8th grade class receive two grades. They are all enrolled in an algebra class as well as a geometry class. We treat the algebra class as the "grade level" basic skills class and the geometry class is the "advanced" class. The geometry we are doing is analytical so students are having to use the algebra at a much higher level...so I'm ok with not making them jump through hoops in the algebra class.
Note: My department is awesome. I truly loved my math department at my previous school and it was really tough to leave them. However, I couldn't imagine working with a group of teachers more willing to try new things. We have pretty good discussions in our department meetings and there is plenty push back. But at the end of the day, we are all trying to find the best way to educate our students.
We decided a few years ago that the sequence of our texts don't really work for us. As a result, we began teaching one standard at a time. We have taken our state standards set up a sequence and pace in a way that makes sense to us. Some of the standards we have broken down into specific skills and these skills are what make up our gradebook.
Common Formative Assessment
Once we have done our initial classroom instruction, we give a common multiple choice assessment. This assessment is graded on a 1-4 rubric. A students next step is based on how well they do on the assessment which is a pretty fair cross-section of the different problems a student may be expect to do on the given standard. We determine the initial score based on the percentage of problems they get correct. 85-100% = 4, 70-84% = 3, 55-69% = 2 and below 55% = 1.
Less Than Proficient
The level of understand a student demonstrates determines what happens next. If a student scores a 1 or 2, he will do a series of activities that may include defining basic terms and demonstrating pre-requisite skills. Once finished with these activities, the student will then take the problems that were missed on the CFA and not only correct them, but explain what went wrong (verbally or in writing) and how to work the problem correctly. Students who score a 3 on the initial assessment are just required to make the necessary corrections with explanation. Once the corrections have been made, the student is then given a re-assessment and the new score replaces the old score in the gradebook.
Proficient
Although students may get 100% of the problems correct on the initial assessment, we still give them a 4. Our reasoning is that the multiple choice test doesn't allow our students to demonstrate understanding that goes beyond classroom instruction, but it does allow them to show proficient understanding. Students who demonstrate proficient understanding on the assessment are given the opportunity to turn the 4 into a 5 by choosing from two categories of activities. Examples of activities may be creating a mini lesson, peer tutoring or some other project agreed upon by teacher and student. The second activity is some sort of writing assignment that may require the student to explain the process or describe what skills a student may need in order to be successful with this standard. Once a student has completed these activities and has shown the ability to explain his work the score in the gradebook will be turned into a 5.
Strengths
At this point, I can say that the strengths of this system are:
- Students grade is based on what they understand and not a mere accumulation of points.
- Students are allowed to re-assess and new understanding replaces old understanding in the gradebook.
- Students seem to understand where they are having trouble and what skills they need to remediate.
- Learning has become a conversation between teacher and student because in order to re-assess, student needs to articulate previous misunderstanding and current understanding.
- Students have a choice on when to re-assess. They can work at their own pace.
- Students also have some choice on which activities to do in order to demonstrate understanding.
- The dross has burned off the grade. Students' grades are based on what they understand rather than things like effort, homework or extra credit.
Weaknesses
- Students have to take more ownership of their learning which means they have to un-learn some bad habits. Not sure that it is a weakness in our system specifically or an indictment of the educational system in general.
- Teachers are having to re-think classroom management when students are working on different activities.
- We are having to decide if some of our standards actually lend themselves to "advanced" work or if later standards are the advanced version of some previous standards.
- Need to develop more advanced activities for students to do while working towards a 5. We allow for students to create their own activity as long as it has been agreed upon by the teacher, however many students don't know what to do with that kind of freedom.
Questions
- What's the best way to take a series of 1's, 2's, 3's, 4's and 5's that are based on levels of understanding and turn them into a letter grade? Do you use mean, median or mode?
- If we go with some sort of average from 1-5, what percentage do you use for an A, B, C, D or F? Currently we are going with average where > 4.5 = A, > 4.0 = B, > 3.0 = C, > 2.0 = D and <2.0 = F.
Adaptation for the Advanced Class
Because my classes are advanced, I have to adapt this system to suit my students' needs. Basically, I am using the standards as the "basic skills" for my class. I have a posted a series of mathcasts and study guides on each standard and the students are expected to view the online examples and do the problems in the study guide prior to taking the pretest. If a student scores above 90% on the initial assessment, there is no other work to be done on the standard--they receive a 5. Students who score below 90%, need to correct their errors, explain to me that they understand why they made their mistakes and how to fix them. Once I am convinced that they have truly corrected their errors, I give them a second assessment and the new score replaces the old one.
My reason for allowing students to earn a 5 right off the bat is that 90% of our classwork is problem solving that uses the standards as the jumping off point. Students in my 8th grade class receive two grades. They are all enrolled in an algebra class as well as a geometry class. We treat the algebra class as the "grade level" basic skills class and the geometry class is the "advanced" class. The geometry we are doing is analytical so students are having to use the algebra at a much higher level...so I'm ok with not making them jump through hoops in the algebra class.
Note: My department is awesome. I truly loved my math department at my previous school and it was really tough to leave them. However, I couldn't imagine working with a group of teachers more willing to try new things. We have pretty good discussions in our department meetings and there is plenty push back. But at the end of the day, we are all trying to find the best way to educate our students.
Sunday, October 25, 2009
We've Had It All Wrong
There have been quite a few blog posts lately discussing how one would explain to a "non-math" person why a negative times a negative is a positive. I think the reason we have such a hard time explaining it is because it's not true. We need look no further than California's own Nancy Pelosi for the explanation. (Check right around 3:50)
In an interview with CNBC's Maria Bartiromo, Pelosi was asked if the expiration of the Bush tax cuts would amount to a tax increase.
Her response:
"It's not a tax increase. It is eliminating a tax decrease that was there."
So there you have it--eliminating a decrease does not amount to an increase. I had better go fix those lesson plans. Thanks for clearing things up, Ms. Pelosi.
In an interview with CNBC's Maria Bartiromo, Pelosi was asked if the expiration of the Bush tax cuts would amount to a tax increase.
Her response:
"It's not a tax increase. It is eliminating a tax decrease that was there."
So there you have it--eliminating a decrease does not amount to an increase. I had better go fix those lesson plans. Thanks for clearing things up, Ms. Pelosi.
Wednesday, October 14, 2009
Calculator : Arithmetic :: GeoGebra: ?
To tell you the truth, I don't really have a problem with my state's math standards (here and here). I do, however, have a serious problem when the standards become the target rather than the scope through which we aim at the target. So what's the target? What should be the point of math education today? It has become very clear to me that it has never been easier to find correct answers to anything rooted in computation. With WolframAlpha, GeoGebra and all the other resources available, there probably isn't a question we could ask a student where they couldn't quickly look up an answer. When I first started teaching, the big question was whether or not we should let our algebra students use a calculator. A lot of the "veteran" teachers were dead set against it because they "gotta add, subtract, multiply and divide, for cryin' out loud." But the calculator would allow a student to speed up all the calculations (read arithmetic) and get to the "math." Well can't the same be said for WolframAlpha or GeoGebra? Don't these tools give students access to certain problems where previously they would have been bogged down by calculations they couldn't complete?
I remember when basic skills were being able to perform the four operations over the Real Number system. What's a basic skill look like today? Is algebra the arithmetic of the 21st century?
I remember when basic skills were being able to perform the four operations over the Real Number system. What's a basic skill look like today? Is algebra the arithmetic of the 21st century?
Monday, October 5, 2009
Who Gets It?
Here's the problem:
An airplane is flying at 36,000 feet directly above Lincoln, Nebraska. A little later the plane is flying at 28,000 feet directly above Des Moines, Iowa, which is 160 miles from Lincoln. Assuming a constant rate of descent, predict how far from Des Moines the airplane will be when it lands. [1]
Question: Which student demonstrates better understanding? Why?




[1] Problem courtesy of Phillips Exeter Academy. Hat Tip: Alison Blank
An airplane is flying at 36,000 feet directly above Lincoln, Nebraska. A little later the plane is flying at 28,000 feet directly above Des Moines, Iowa, which is 160 miles from Lincoln. Assuming a constant rate of descent, predict how far from Des Moines the airplane will be when it lands. [1]
Question: Which student demonstrates better understanding? Why?
Student A

Student B

Student C

Student D

[1] Problem courtesy of Phillips Exeter Academy. Hat Tip: Alison Blank
Saturday, October 3, 2009
Intro To Problem Solving
A while back, Justin Tolentino had a post asking how others might go about teaching problem solving strategies. Great question. I have started and scrapped a couple of responses to his post as well as a posts of my own on this topic. I think the easiest way for me to describe it is in the question I gave my 7th graders this morning.
A man lives on the 10th floor of a building. Each time he leaves his building, he will take the elevator from the 10th floor to the 1st floor. However, when he returns, he will take the elevator to the 7th floor and walk the remaining three flights to his apartment. Why does he do this?
I am sure that many of you have heard this lateral thinking puzzle before and may wonder how it belongs in a math class. I realize that this problem has nothing to do with math, but in my opinion, neither does problem solving. We use math as a vehicle to teach students how to take information they are given and then discern that which they can use and that which they must refuse. From there they can ask questions to gain any new information they need in order to solve the problem.
The only requirements I give students the first time I ask them one of these puzzles is that they ask "yes or no" questions. I also tell them that my answer to their questions will either be "yes, no or irrelevant." Then I turn them loose.
They start firing random questions like crazy.
"Is he afraid of heights?"
"Does the elevator work?"
"Does he need the exercise?"
These questions come in all shapes and sizes and many of them are very specific. After about 10 questions, I tell them I'm only going to give them 21 questions and I make a mark on the board after each question. At first, it doesn't deter them. They keep at it, often times repeating a question that was already asked. Then they get to about 15 and someone suggests that they slow down a bit and start thinking about what to ask next. Today, we got to 21 with no resolution and I was about to walk away from it when one of the kids who knew the answer asked if he could ask a question.
Sure.
"Does he have to walk the remaining three flights?"
"Yes he does. And if you guys would have asked this question in the beginning, it would have kept you from having to waste some of your other questions."
This brings us to a great discussion on how we can look at a problem and ask general questions that eliminate the need to ask other more specific questions. As we carve out large chunks of potential questions, we begin to narrow our focus and become more specific.
I really like what I see when I present these puzzles to my students. Kids who won't normally offer much in a class discussion, will often times ask really good thoughtful questions. They feel safe to do so because the given information is so limited, there is no way to feel "stupid" for not knowing the answer. In fact, the entire process assumes that no one knows the answer.
This leads me to ask: How can we get students comfortable with what they don'tknow? How do we convince them that being educated isn't about knowing all the answers; it's about asking the right questions?
A man lives on the 10th floor of a building. Each time he leaves his building, he will take the elevator from the 10th floor to the 1st floor. However, when he returns, he will take the elevator to the 7th floor and walk the remaining three flights to his apartment. Why does he do this?
I am sure that many of you have heard this lateral thinking puzzle before and may wonder how it belongs in a math class. I realize that this problem has nothing to do with math, but in my opinion, neither does problem solving. We use math as a vehicle to teach students how to take information they are given and then discern that which they can use and that which they must refuse. From there they can ask questions to gain any new information they need in order to solve the problem.
The only requirements I give students the first time I ask them one of these puzzles is that they ask "yes or no" questions. I also tell them that my answer to their questions will either be "yes, no or irrelevant." Then I turn them loose.
They start firing random questions like crazy.
"Is he afraid of heights?"
"Does the elevator work?"
"Does he need the exercise?"
These questions come in all shapes and sizes and many of them are very specific. After about 10 questions, I tell them I'm only going to give them 21 questions and I make a mark on the board after each question. At first, it doesn't deter them. They keep at it, often times repeating a question that was already asked. Then they get to about 15 and someone suggests that they slow down a bit and start thinking about what to ask next. Today, we got to 21 with no resolution and I was about to walk away from it when one of the kids who knew the answer asked if he could ask a question.
Sure.
"Does he have to walk the remaining three flights?"
"Yes he does. And if you guys would have asked this question in the beginning, it would have kept you from having to waste some of your other questions."
This brings us to a great discussion on how we can look at a problem and ask general questions that eliminate the need to ask other more specific questions. As we carve out large chunks of potential questions, we begin to narrow our focus and become more specific.
I really like what I see when I present these puzzles to my students. Kids who won't normally offer much in a class discussion, will often times ask really good thoughtful questions. They feel safe to do so because the given information is so limited, there is no way to feel "stupid" for not knowing the answer. In fact, the entire process assumes that no one knows the answer.
This leads me to ask: How can we get students comfortable with what they don'tknow? How do we convince them that being educated isn't about knowing all the answers; it's about asking the right questions?
Thursday, October 1, 2009
Thoughts I Have While Brushing My Teeth
What Are You Looking At?
Today I gave my classes a survey as a way to gain some feedback on how the first quarter has gone. One of the questions was "What would make you more comfortable asking questions in class?"
Here is the response that really pushed back:
WOW! I had never really thought of that. Yeah, I guess if I am burning a whole through a kid with my gaze while I am answering a question, it may just make them think twice about asking another one. I don't think I do that, but perception is reality to these kids. So if she says I do it, I guess I do. Need to keep a watch out for that one.
Where do you look when you are answering a question from a student?
Here is the response that really pushed back:
Well, this may seem silly and childish, but you want the truth, right?
Well, when a student asks a question, you seem to direct your answer to the person who asked it, which makes me feel uncomfortabe. I mean, if other people don't understand, then why only talk to one person, instead of the whole class? It makes me feel weird, like I'm the only one who doesn't understand, and the teacher looking at one single student seems to cause everyone to look, making the student even MORE uncomfortable. As I read over this, I feel I want to delete it, because it seems so silly and unnecessary of mentioning. I won't delete it, I guess, because I suppose you want to know this, no matter how silly it (mine) is.
WOW! I had never really thought of that. Yeah, I guess if I am burning a whole through a kid with my gaze while I am answering a question, it may just make them think twice about asking another one. I don't think I do that, but perception is reality to these kids. So if she says I do it, I guess I do. Need to keep a watch out for that one.
Where do you look when you are answering a question from a student?
Wednesday, September 23, 2009
What's in a Grade?
"How many pages does it have to be?"
"Is this going to count?"
"How many points is it worth?"
"What can I do to bring my grade up?"
"Can I do extra credit?"
You've all heard these before, right? I have said for a long time that the worst part of teaching is grading. It's a tough situation because somehow we have to put a number on it. If we don't grade, then "kids won't do it." But because of grades, we often get students who are looking for the least amount of work for the maximum grade. I hate that about this job. I want to ask questions that lead them to ask questions and have class end up with a giant group hug where we all walk away realizing that we may not know the answers, but man, we sure questioned the heck out of it.
We have done a lot of work on our campus to try to get kids to go beyond the curriculum. We just became the first middle school in our county to reach 800 in API. Yeah, hold the applause. It's based on a standardized test which we all know don't mean nuthin' when it comes to having kids actually think. But truth be known, this means that principals from our area will come calling asking, "what are you guys doing?" They may be disappointed when they come to see the dog and pony show but end up seeing a staff that is doing their darndest to get kids to question and speak/write complete thoughts. You see, these principals are asking the wrong question. It isn't about what we are doing. It's about what the kids are doing.
Apparently our students are doing something right, though. They are developing a reputation in high school for being "Sequoia kids" who sit in the front row, ask questions and, at times, challenge an occasional teacher to step up their game. Fantastic! But how do you grade that? How do you grade a kid who has learned how to learn? Last I checked, that isn't in my state framework. There's no standard for that. Which brings me back to grades.
How do you quantify learning? Why is 90% average the accepted norm for a kid who really gets it? 90% of what? Is this student truly advanced, or did she take a bunch of tests full of a bunch of basic questions and get 90% of them correct?
So tell me, what does a kid have to do to earn an A in your class? What are you doing to ensure that the grade actually means something and isn't just verification that a student jumped through all the right hoops?
"Is this going to count?"
"How many points is it worth?"
"What can I do to bring my grade up?"
"Can I do extra credit?"
You've all heard these before, right? I have said for a long time that the worst part of teaching is grading. It's a tough situation because somehow we have to put a number on it. If we don't grade, then "kids won't do it." But because of grades, we often get students who are looking for the least amount of work for the maximum grade. I hate that about this job. I want to ask questions that lead them to ask questions and have class end up with a giant group hug where we all walk away realizing that we may not know the answers, but man, we sure questioned the heck out of it.
We have done a lot of work on our campus to try to get kids to go beyond the curriculum. We just became the first middle school in our county to reach 800 in API. Yeah, hold the applause. It's based on a standardized test which we all know don't mean nuthin' when it comes to having kids actually think. But truth be known, this means that principals from our area will come calling asking, "what are you guys doing?" They may be disappointed when they come to see the dog and pony show but end up seeing a staff that is doing their darndest to get kids to question and speak/write complete thoughts. You see, these principals are asking the wrong question. It isn't about what we are doing. It's about what the kids are doing.
Apparently our students are doing something right, though. They are developing a reputation in high school for being "Sequoia kids" who sit in the front row, ask questions and, at times, challenge an occasional teacher to step up their game. Fantastic! But how do you grade that? How do you grade a kid who has learned how to learn? Last I checked, that isn't in my state framework. There's no standard for that. Which brings me back to grades.
How do you quantify learning? Why is 90% average the accepted norm for a kid who really gets it? 90% of what? Is this student truly advanced, or did she take a bunch of tests full of a bunch of basic questions and get 90% of them correct?
So tell me, what does a kid have to do to earn an A in your class? What are you doing to ensure that the grade actually means something and isn't just verification that a student jumped through all the right hoops?
Thursday, September 17, 2009
I'm Telling Ya, Lesson Plans are Overrated.
This year, I have kind of introduced equation solving to my 7th graders very informally. One way I have done this is by giving them a few balance equations like this:
It seems like it takes the edge off when the variable isn't there. But today one of our warmup problems was: 5x + 1 = 2x + 7.
I have been amazed at how many of my students have been willing to attack equation solving by using a guess and check table. I've never taught it that way, but some kids have just taken to it. After today, I may start to encourage it. One kid noticed that when you let x=1, the right side is greater than the left side. But if you let x=10, the left side is greater. When the balance of power shifts, you know that the answer is between your last two guesses. Of course, typical guess and check strategy. But the thing I like about it when dealing with these linear equations is that they are beginning to think in terms of linear systems and how the point of intersection acts as a dividing point between which equation has greater value. They're teaching me something.
But Brandon took the cake. He says, "Mr. Cox, you can tell the left side is going to be 6 because 5+1=6 and the right side is going to be 9 because 2+7=9."
"What does x have to be for that to be true?"
"X=1. But as we make changes to x, the other one is growing faster."
"How fast is it growing?"
"The left side is growing by 5 and the right side is growing by 2. So eventually, we know that the left side is going to be greater than the right side."
"Yeah. So when are the 1 and the 7 important?"
"Only at the beginning."
It took all the self control I could muster to keep from talking about initial condition or rate of change at this point. I'm glad I didn't because I think I would have ruined an authentic learning moment for this kid. The thing I wanted to encourage the most in him was the fact that he looked for patterns and then asked questions to help make sense of those patterns.
One warmup which I expected to spend 5 minutes on turns into 20 minutes of slope, y-intercept, linear systems and problem solving strategies all because a few students took an approach I've never taught.
Another example of the kids re-writing the lesson plan.

It seems like it takes the edge off when the variable isn't there. But today one of our warmup problems was: 5x + 1 = 2x + 7.
I have been amazed at how many of my students have been willing to attack equation solving by using a guess and check table. I've never taught it that way, but some kids have just taken to it. After today, I may start to encourage it. One kid noticed that when you let x=1, the right side is greater than the left side. But if you let x=10, the left side is greater. When the balance of power shifts, you know that the answer is between your last two guesses. Of course, typical guess and check strategy. But the thing I like about it when dealing with these linear equations is that they are beginning to think in terms of linear systems and how the point of intersection acts as a dividing point between which equation has greater value. They're teaching me something.
But Brandon took the cake. He says, "Mr. Cox, you can tell the left side is going to be 6 because 5+1=6 and the right side is going to be 9 because 2+7=9."
"What does x have to be for that to be true?"
"X=1. But as we make changes to x, the other one is growing faster."
"How fast is it growing?"
"The left side is growing by 5 and the right side is growing by 2. So eventually, we know that the left side is going to be greater than the right side."
"Yeah. So when are the 1 and the 7 important?"
"Only at the beginning."
It took all the self control I could muster to keep from talking about initial condition or rate of change at this point. I'm glad I didn't because I think I would have ruined an authentic learning moment for this kid. The thing I wanted to encourage the most in him was the fact that he looked for patterns and then asked questions to help make sense of those patterns.
One warmup which I expected to spend 5 minutes on turns into 20 minutes of slope, y-intercept, linear systems and problem solving strategies all because a few students took an approach I've never taught.
Another example of the kids re-writing the lesson plan.
Tuesday, September 15, 2009
SHOW YOUR WORK!
I've been getting real tired of having to sift through my students chicken scratch to find the few nuggets of information they have hidden in their "work." It kind of came to a head the other night as I was grading our most recent geometry test. It became clear that many of these students really have not been taught what it means to show work in a clear and organized manner. I have modeled it many times, pointing out how one should line up the equal signs, how arithemetic isn't necessarily showing work, etc. However, I think that when I've tried to explain this, all they hear is Charlie Brown's teacher. "Wha wha wha...wha wha whaa."
I decided to give them a taste of their own medicine. I took the warm up I had planned and dumped it into Wordle (I figured Wordle must be good for something). Yesterday's warm up:

"But Mr. Cox, what are we supposed to do?"
"The directions are all there. It's worth 100 pts. you know, so ya better make it snappy."
"It's hard to understand."
"Ok, you don't like this one; how about this?"
"That's no better."
"No?"
They're on to me by now.
"Yeah, of course I'm proving a point; but what is it?"
The conversation went something like this:
"You think this is confusing? Well that's what you do to me whenever you show your work. Why is it that in your Language Arts classes you all understand that we start writing in the top left, we work left to right and top down, but in your math class, you seem to think that starting right in the center of your workspace and then going any which way is a good idea? How in the world am I supposed to understand what you're telling me?"
So I threw up some examples of what to do...
and what not to do...

and we discussed what made one student's work acceptable and the other's unacceptable. We also discussed the difference between "showing your work" or "showing your steps" and that which belongs on scratch paper.
Oh, we also agreed that starting in the upper left hand corner of the workspace is acceptable in a math class as well.
I decided to give them a taste of their own medicine. I took the warm up I had planned and dumped it into Wordle (I figured Wordle must be good for something). Yesterday's warm up:

"But Mr. Cox, what are we supposed to do?"
"The directions are all there. It's worth 100 pts. you know, so ya better make it snappy."
"It's hard to understand."
"Ok, you don't like this one; how about this?"

"That's no better."
"No?"
They're on to me by now.
"Yeah, of course I'm proving a point; but what is it?"
The conversation went something like this:
"You think this is confusing? Well that's what you do to me whenever you show your work. Why is it that in your Language Arts classes you all understand that we start writing in the top left, we work left to right and top down, but in your math class, you seem to think that starting right in the center of your workspace and then going any which way is a good idea? How in the world am I supposed to understand what you're telling me?"
So I threw up some examples of what to do...

and what not to do...

and we discussed what made one student's work acceptable and the other's unacceptable. We also discussed the difference between "showing your work" or "showing your steps" and that which belongs on scratch paper.
Oh, we also agreed that starting in the upper left hand corner of the workspace is acceptable in a math class as well.
Friday, September 11, 2009
Monologue to Dialogue
"When you add a positive integer with a negative integer, how do you know if your answer is positive or negative?"
"Well if the negative number is bigger, then the answer is going to negative. If the positive number is bigger, then the answer is positive."
"Aren't all positive numbers bigger than negative numbers?"
"Well, yeah. But if you take the sign off the negative and it's bigger than the positive, then the answer will be negative."
"Why are you taking the sign off the negative number? What rule allows you to do that?"
"Uhh..."
"I know that I can give you 20 addition problems and you will probably get all 20 right, but I want you to explain to me why this works the way it does. Come talk to me when you think you have an answer."
*10 minutes goes by*
"Alright, I think I've got it. If the negative number is farther down the number line than the positive number, then the answer is going to be negative."
"Farther down the number line?"
"Yeah, it's more negative than the positive number is positive."
"How do you know that?"
"It's farther from zero?"
"Oh, what do we call that when a number is farther from zero than another number?"
"Uhh..."
*5 minutes later*
"ABSOLUTE VALUE!. If the negative number has a greater absolute value, then the answer is negative. If the positive number has the greater absolute value, then the answer is positive."
"That is correct young grasshopper. You have done well. You may now enter into the realm of proficiency."
I have had this conversation about 10 times over the last few days. Our current system has students take a common formative assessment (CFA)which is very closely aligned to our state's standards. It's a multiple choice test that has questions that look an awful lot like the same questions they'll be seeing in April when we take the CST test. Based on their score, they have a set of activities to do before they can re-assess. Re-assessment may look like the conversation above. I think I am really going to like this system because it allows for dialogue between teacher and student. I have the opportunity to ask them about the why and actually tie it to their grade. The benefit to this is that students have choice in how they demonstrate their proficiency the second time. The first time, it's a multiple choice test. However, the second time may be written, oral or heck, they may even draw a picture. One of the best things about this is that the students are taking more ownership of their learning because they have to direct some of the activities. They actually have choice. And that's empowering. They aren't waiting for me to give them another hoop to jump through.
The parents are coming along slowly. Many of them didn't understand how their student could score 100% on the CFA and yet the score in the grade book shows up as 80%. Last night was Back to School Night and I got the chance to explain that each standards' assessment is two parts. The first part is multiple choice and the second part depends on the student. Once they realized that their child's grade quits improving when they quit trying, I think they got it.
It'd be nice if we could focus less on the grade and more on learning, but...
...baby steps.
"Well if the negative number is bigger, then the answer is going to negative. If the positive number is bigger, then the answer is positive."
"Aren't all positive numbers bigger than negative numbers?"
"Well, yeah. But if you take the sign off the negative and it's bigger than the positive, then the answer will be negative."
"Why are you taking the sign off the negative number? What rule allows you to do that?"
"Uhh..."
"I know that I can give you 20 addition problems and you will probably get all 20 right, but I want you to explain to me why this works the way it does. Come talk to me when you think you have an answer."
*10 minutes goes by*
"Alright, I think I've got it. If the negative number is farther down the number line than the positive number, then the answer is going to be negative."
"Farther down the number line?"
"Yeah, it's more negative than the positive number is positive."
"How do you know that?"
"It's farther from zero?"
"Oh, what do we call that when a number is farther from zero than another number?"
"Uhh..."
*5 minutes later*
"ABSOLUTE VALUE!. If the negative number has a greater absolute value, then the answer is negative. If the positive number has the greater absolute value, then the answer is positive."
"That is correct young grasshopper. You have done well. You may now enter into the realm of proficiency."
I have had this conversation about 10 times over the last few days. Our current system has students take a common formative assessment (CFA)which is very closely aligned to our state's standards. It's a multiple choice test that has questions that look an awful lot like the same questions they'll be seeing in April when we take the CST test. Based on their score, they have a set of activities to do before they can re-assess. Re-assessment may look like the conversation above. I think I am really going to like this system because it allows for dialogue between teacher and student. I have the opportunity to ask them about the why and actually tie it to their grade. The benefit to this is that students have choice in how they demonstrate their proficiency the second time. The first time, it's a multiple choice test. However, the second time may be written, oral or heck, they may even draw a picture. One of the best things about this is that the students are taking more ownership of their learning because they have to direct some of the activities. They actually have choice. And that's empowering. They aren't waiting for me to give them another hoop to jump through.
The parents are coming along slowly. Many of them didn't understand how their student could score 100% on the CFA and yet the score in the grade book shows up as 80%. Last night was Back to School Night and I got the chance to explain that each standards' assessment is two parts. The first part is multiple choice and the second part depends on the student. Once they realized that their child's grade quits improving when they quit trying, I think they got it.
It'd be nice if we could focus less on the grade and more on learning, but...
...baby steps.
Tuesday, September 8, 2009
I'm Lovin' This!
A couple of weeks ago, I posted a question regarding how I should handle my advanced 8th grade class. I got a bunch of great responses which cemented my opinion that these PLN's are no joke. In a matter of hours, I got a responses from Kate Nowak (telling me to pull my head out and quit encouraging this "jump through hoops" mentality), Darren Kuropatwa (detailing some great extension lessons as well as some online resources), a tweet from Jackie Ballarini (suggesting that I go with an analytical approach to geometry) and an email from Alison Blank(offering a problem based analytical geometry curriculum). By the end of the weekend, I was in conversation with Alison and Jim Wysocki regarding the geometry curriculum.
This problem based geometry is good stuff. It is rigorous, but the skills the kids need are all review. We may only get through 10-12 problems every day or two, but they are really causing them to think. That's good, right?
Anyway, this allows me to try to implement something I have been working on for a while. Chris Lehmann called it "inverting the classroom." I like the idea because it allows me to have kids work on the skills review outside of class while we spend the class time discussing the meaty stuff; the problems that make our heads explode only to find out that if I would have just stepped back and taken a different look at the problem, there is a simple yet elegant way to solve it.
I can see two camps evolving in the class. Those who embrace the problem solving and those who feel like they can't do it. I'll keep you posted on how it goes. But, so far, so good.
Thanks again.
This problem based geometry is good stuff. It is rigorous, but the skills the kids need are all review. We may only get through 10-12 problems every day or two, but they are really causing them to think. That's good, right?
Anyway, this allows me to try to implement something I have been working on for a while. Chris Lehmann called it "inverting the classroom." I like the idea because it allows me to have kids work on the skills review outside of class while we spend the class time discussing the meaty stuff; the problems that make our heads explode only to find out that if I would have just stepped back and taken a different look at the problem, there is a simple yet elegant way to solve it.
I can see two camps evolving in the class. Those who embrace the problem solving and those who feel like they can't do it. I'll keep you posted on how it goes. But, so far, so good.
Thanks again.
Wednesday, September 2, 2009
What's the point?
One of my favorite activities is to have students draw a point on a paper and see how many distinct lines they can draw through the point. I usually set it up as a competition to see who can get the most lines inside of 15 seconds or so. On your mark, get set, GO! Pencils start flying.
Then to bring the lesson home, I say, "Alright, flip the paper over and put two points on the page. Now we're gonna see who can get the most lines through both points."
Ready, set, GO!
They get the first line fast. Then they panic as they move the ruler and pencil searching for that elusive second line. Most of 'em end up looking something like this:
I tease them a bit and we all get a good chuck out of it. I know, I know. It's not nice to take advantage of these trusting impressionable children. But I don't care who you are, that thar's funny!
And, they never forget it.
Then to bring the lesson home, I say, "Alright, flip the paper over and put two points on the page. Now we're gonna see who can get the most lines through both points."
Ready, set, GO!
They get the first line fast. Then they panic as they move the ruler and pencil searching for that elusive second line. Most of 'em end up looking something like this:

I tease them a bit and we all get a good chuck out of it. I know, I know. It's not nice to take advantage of these trusting impressionable children. But I don't care who you are, that thar's funny!
And, they never forget it.
Saturday, August 29, 2009
How Close is Close Enough?
For my 8th graders, homework for day 2 consisted of a worksheet where students determined which set(s) included given numbers. Pretty easy stuff. But I threw one of my favorite problems at 'em to see what they'd do with it.
What's the sum of 1/2 + 1/4 + 1/8...?
At first they're thinking, "not possible 'cause it goes on forever." I told them to try it anyway.
The two most popular answers were ".99..." and "1." But those who answered "1" were quick to admit that they just rounded off. We open the discussion and I was very pleased with how thoughtful and respectful everyone was. These kids were really interested in getting to the bottom of this. It was a great opportunity to demonstrate that often times drawing a picture will allow you to see things in a problem that you may not otherwise catch.
So we draw a square on the board and shade 1/2. Then we shade 1/4, then 1/8 and so on. They soon see that the square will eventually be full.
Me: "So is it 1 or is it just really close?"
"Really close. Because the square is never completely full. You always have half of the remaining area that is unshaded."
Good. So let's see how they handle this.
"Alright, what's 1/3 as a decimal?"
".333..."
"Ok, and how about 2/3?"
".666..."
"what's 1/3 + 2/3?"
"1."
"And what's .333...+ .666..."
".999..."
"So does .999... = 1 or is it just really close?"
At this point they admit that it looks like it's equal but it just doesn't make sense. Time to to talk about what it means to be infinitely close to something. This is always a fascinating discussion. We discussed the idea of a neighborhood and how if .999... does not equal 1, then there must be a number between them.
"Give me the number and I'll shut up", I tell them.
One kid says," How about .0 with a repetend, then a 1?"
But another student catches this, "If the zero goes forever, when do we add the 1?"
It amazes me how these kids can grapple with the real "stuff" that is mathematics. These same questions that got me hooked as I was taking my analysis classes in college are finding their way into the minds of 8th graders. And you know what? They get it...at least as much as they possibly can.
Man, I love this job!
What's the sum of 1/2 + 1/4 + 1/8...?
At first they're thinking, "not possible 'cause it goes on forever." I told them to try it anyway.
The two most popular answers were ".99..." and "1." But those who answered "1" were quick to admit that they just rounded off. We open the discussion and I was very pleased with how thoughtful and respectful everyone was. These kids were really interested in getting to the bottom of this. It was a great opportunity to demonstrate that often times drawing a picture will allow you to see things in a problem that you may not otherwise catch.
So we draw a square on the board and shade 1/2. Then we shade 1/4, then 1/8 and so on. They soon see that the square will eventually be full.
Me: "So is it 1 or is it just really close?"
"Really close. Because the square is never completely full. You always have half of the remaining area that is unshaded."
Good. So let's see how they handle this.
"Alright, what's 1/3 as a decimal?"
".333..."
"Ok, and how about 2/3?"
".666..."
"what's 1/3 + 2/3?"
"1."
"And what's .333...+ .666..."
".999..."
"So does .999... = 1 or is it just really close?"
At this point they admit that it looks like it's equal but it just doesn't make sense. Time to to talk about what it means to be infinitely close to something. This is always a fascinating discussion. We discussed the idea of a neighborhood and how if .999... does not equal 1, then there must be a number between them.
"Give me the number and I'll shut up", I tell them.
One kid says," How about .0 with a repetend, then a 1?"
But another student catches this, "If the zero goes forever, when do we add the 1?"
It amazes me how these kids can grapple with the real "stuff" that is mathematics. These same questions that got me hooked as I was taking my analysis classes in college are finding their way into the minds of 8th graders. And you know what? They get it...at least as much as they possibly can.
Man, I love this job!
Friday, August 28, 2009
Is This Wrong?
In a 6-1 vote, the Los Angeles City Board of Education decided to turn over 250 of its schools over to charter and other private operators. I'll definitely watch this story unfold with tremendous interest. Although I don't really understand all the ramifications of such a decision. I have to ask: Is This Wrong?
Is turning schools to charter groups and/or private operators going to foster competition and if so, is that a bad thing?
Will this help turn teaching into a profession where innovation is rewarded?
Do the teachers' unions actually have students' best interests at heart?
Who stands to profit from this? And do these folks care about education as much as they care about making money?
Some have said that this is a direct result of high stakes testing and the one-size-fits-all philosophy of education that inevitibly Leaves Children Behind.
But were we doing such a good job before NCLB and the high stakes test?
I don't know, but I'm curious.
Is turning schools to charter groups and/or private operators going to foster competition and if so, is that a bad thing?
Will this help turn teaching into a profession where innovation is rewarded?
Do the teachers' unions actually have students' best interests at heart?
Who stands to profit from this? And do these folks care about education as much as they care about making money?
Some have said that this is a direct result of high stakes testing and the one-size-fits-all philosophy of education that inevitibly Leaves Children Behind.
But were we doing such a good job before NCLB and the high stakes test?
I don't know, but I'm curious.
Wednesday, August 26, 2009
Teacher of the Year: Stevie Wonder
When I was about 12 years old, my parents took my brother and I to see Stevie Wonder in concert. It was my first real concert experience and most of it is now a blur. But 25 years later, the one thing that sticks out in my mind turns out to be something that had nothing to do with Stevie Wonder's music. It had to do with a lady in the front row who couldn't carry a tune if it were strapped to her back.
About half way through the concert, Stevie (or is it Mr. Wonder?) interacts with the crowd and decides to hold a singing contest. He gets three volunteers from the crowd and they each get a turn singing Satisfaction by the Rolling Stones. The winner gets to sing the song of his choice with Stevie Wonder himself. Talk about the opportunity of a lifetime.
Two of the three could sing very well, but I don't really remember much about their performances. However, the third contestant was very sharp. So much so, that even my untrained ear could tell that this lady couldn't sing. Here is the impressive part: in the middle of her singing, Stevie Wonder stops the band and has them adjust the key of the music to fit her voice. He recognized the exact key in which she was singing and made the adjustment to fit her. It did't work--she still stunk, but that isn't the point.
As teachers, we need to do the exact same thing every day. No matter how well we construct a lesson, we need to be ready to adjust to the kid who continues to sing off key. You can't plan for that. The band didn't practice the song in every possible key just in case they had someone who couldn't sing with them. They knew their song, they understood the progression and understood what to do if they started somewhere different than where they had planned.
I believe that an effective teacher is going to be the one who can recognize where a student is in relation to where the objective is, meet him where he is and adjust the plan accordingly. It's not so much about having a great engaging plan all the time. We can plan a symphonic lesson plan in which all the small parts fit together into a wonderful investigation or lecture. But it's what we do when the kid playing the oboe doesn't hear what everyone else hears and plays the wrong notes that really matters.
About half way through the concert, Stevie (or is it Mr. Wonder?) interacts with the crowd and decides to hold a singing contest. He gets three volunteers from the crowd and they each get a turn singing Satisfaction by the Rolling Stones. The winner gets to sing the song of his choice with Stevie Wonder himself. Talk about the opportunity of a lifetime.
Two of the three could sing very well, but I don't really remember much about their performances. However, the third contestant was very sharp. So much so, that even my untrained ear could tell that this lady couldn't sing. Here is the impressive part: in the middle of her singing, Stevie Wonder stops the band and has them adjust the key of the music to fit her voice. He recognized the exact key in which she was singing and made the adjustment to fit her. It did't work--she still stunk, but that isn't the point.
As teachers, we need to do the exact same thing every day. No matter how well we construct a lesson, we need to be ready to adjust to the kid who continues to sing off key. You can't plan for that. The band didn't practice the song in every possible key just in case they had someone who couldn't sing with them. They knew their song, they understood the progression and understood what to do if they started somewhere different than where they had planned.
I believe that an effective teacher is going to be the one who can recognize where a student is in relation to where the objective is, meet him where he is and adjust the plan accordingly. It's not so much about having a great engaging plan all the time. We can plan a symphonic lesson plan in which all the small parts fit together into a wonderful investigation or lecture. But it's what we do when the kid playing the oboe doesn't hear what everyone else hears and plays the wrong notes that really matters.
Tuesday, August 25, 2009
Dear Sam,
Just read your post about being a fraud and you hit the nail on the head. But you may not have hit the nail you were aiming at. You a fraud? Come on! I have never met you but I can hear your voice with every sentence you write. You can't fake that.
You know what I'd expect if I came to see you teach? I'd expect to see a guy who cares about his students both in and out of class. I'd expect to see a teacher who does his best to reach his students where they are, lift them to where they need to be and encourage them to become what they could be. I'm pretty sure Socrates didn't have lesson plans and we're still talking about him. All he did was ask questions. I'm pretty sure you do that too.
Don't worry about putting your best stuff out there for all of us to see. We all clean up the house when we have company over. Every time you post, you are inviting us to your classroom. Thanks for that.
So before you beat yourself up about not being where you want to be, remember this: None of us are! That's the nail you hit. We all keep striving in this game and none of us has completely figured it out; we merely get glimpses of what could be. And anyone who tells you otherwise is the real fraud. It took me 14 years of teaching to get to where I am and I still make rookie mistakes, have lessons that flop, get irritated with kids who won't engage and still don't exactly know what to do with kids who are bored.
So thanks for the honesty, but sometimes we get tangled up in the accidents and forget the essence. At your essence, you're a teacher; plain and simple.
Best to you this year.
David
p.s. Now if I find out that you're not really a teacher and all you did was stay at a Holiday Inn Express last night, then I'm gonna be pissed.
You know what I'd expect if I came to see you teach? I'd expect to see a guy who cares about his students both in and out of class. I'd expect to see a teacher who does his best to reach his students where they are, lift them to where they need to be and encourage them to become what they could be. I'm pretty sure Socrates didn't have lesson plans and we're still talking about him. All he did was ask questions. I'm pretty sure you do that too.
Don't worry about putting your best stuff out there for all of us to see. We all clean up the house when we have company over. Every time you post, you are inviting us to your classroom. Thanks for that.
So before you beat yourself up about not being where you want to be, remember this: None of us are! That's the nail you hit. We all keep striving in this game and none of us has completely figured it out; we merely get glimpses of what could be. And anyone who tells you otherwise is the real fraud. It took me 14 years of teaching to get to where I am and I still make rookie mistakes, have lessons that flop, get irritated with kids who won't engage and still don't exactly know what to do with kids who are bored.
So thanks for the honesty, but sometimes we get tangled up in the accidents and forget the essence. At your essence, you're a teacher; plain and simple.
Best to you this year.
David
p.s. Now if I find out that you're not really a teacher and all you did was stay at a Holiday Inn Express last night, then I'm gonna be pissed.
Monday, August 24, 2009
The Evolution of the Mathcast
Two years ago my principal approached me about getting a SmartBoard for each of the math teachers in my department. I had no idea what he was talking about. Heck, before I came here, my daily tech decision was: Vis-a-Vis or Expo? So when he starts talking about this board that lets you interact with the computer whose screen is projected back on the board, I think my head almost exploded. Didn't have a clue how I'd use it. Against my better judgement, he ordered them anyway. They came in a couple of weeks before school started, I helped him install one on my wall and off I went. No training, no direction. Just me and my computer.
I particularly appreciated the ease by which I could do the drawings and graphs which were such a drag with an overhead. I hated to give up my vintage set of chalk board drawing tools, but it had to happen. A guy's gotta grow up some time. As I was toying around with some of the features, I noticed that there was what looked like a record button. We played around with the thing and figured out how to record the annotations but had a tough time getting the sound to record. I played with the settings and in walks a wireless lapel mic. Got it up and running and away I went.
At first the recordings were a train wreck (I'm still not completely pleased with the quality of some of the examples). The default file was .avi and I would post the lessons through the school website. The problem was a student would click the link, go make a sandwich, do the dishes and come back just in time for the recording to play. One of our district IT guys suggested I compress the .avi in MovieMaker to allow it to open faster. Keep in mind, I really had no idea what I was doing. I was basically swinging at pitches in the dirt hoping to connect. Anyway, I had my first examples online ready to view by Christmas.
Man, we thought we were cutting edge. Then last year, I stumbled upon Tim Fahlberg's wiki. Turns out this guy has been doing mathcasts since I was in high school. He practically invented this stuff. I contacted Tim and he turned me on to Camtasia Studio. It's a bit pricey, but it allows one to render the videos in many different formats. It's also very easy to use. Eventually this led to a channel on blip.tv as well as a podcast through iTunes.
The learning curve has been pretty steep but has started to level off a bit. I am now passed the point of wondering how much can be done with this technology, but now I am wondering how to best use the ability to create dynamic notes for my students. The nice thing about the channel on blip.tv as well as being on iTunes is that kids can subscribe and download the examples so they can take them wherever they go. It's amazing to think that I have kids watching these things on their iPhone's and PSP's. But they are. So the question is how do we best use this tool? Chris Lehmann suggests inversions. What say you?
I particularly appreciated the ease by which I could do the drawings and graphs which were such a drag with an overhead. I hated to give up my vintage set of chalk board drawing tools, but it had to happen. A guy's gotta grow up some time. As I was toying around with some of the features, I noticed that there was what looked like a record button. We played around with the thing and figured out how to record the annotations but had a tough time getting the sound to record. I played with the settings and in walks a wireless lapel mic. Got it up and running and away I went.
At first the recordings were a train wreck (I'm still not completely pleased with the quality of some of the examples). The default file was .avi and I would post the lessons through the school website. The problem was a student would click the link, go make a sandwich, do the dishes and come back just in time for the recording to play. One of our district IT guys suggested I compress the .avi in MovieMaker to allow it to open faster. Keep in mind, I really had no idea what I was doing. I was basically swinging at pitches in the dirt hoping to connect. Anyway, I had my first examples online ready to view by Christmas.
Man, we thought we were cutting edge. Then last year, I stumbled upon Tim Fahlberg's wiki. Turns out this guy has been doing mathcasts since I was in high school. He practically invented this stuff. I contacted Tim and he turned me on to Camtasia Studio. It's a bit pricey, but it allows one to render the videos in many different formats. It's also very easy to use. Eventually this led to a channel on blip.tv as well as a podcast through iTunes.
The learning curve has been pretty steep but has started to level off a bit. I am now passed the point of wondering how much can be done with this technology, but now I am wondering how to best use the ability to create dynamic notes for my students. The nice thing about the channel on blip.tv as well as being on iTunes is that kids can subscribe and download the examples so they can take them wherever they go. It's amazing to think that I have kids watching these things on their iPhone's and PSP's. But they are. So the question is how do we best use this tool? Chris Lehmann suggests inversions. What say you?
Friday, August 21, 2009
What to do...
I have a bit of a dilemma. Three years ago I was brought to a GATE magnet school to teach a bunch of advanced kids.
The thought was, "Rather than ship the really smart kids to high school to take the geometry class, we'll just bring the high school teacher to them."
I didn't mind this idea. In fact, it quickly began to grow on me. I was teaching precalc, algebra 2 and algebra 1 at the high school and figured the change might do me some good. The tough part was that I had no idea what to expect. I was going from 55 minute periods to 94 minute daily blocks.
What the heck am I going to do with a group of middle schoolers for 94 minutes?
So after many discussions with my principal, we decided that since the 94 minute block was intended to allow for grade level instruction as well as time for intervention, I'd just use my extra time for enrichment. But what do you do to enrich them? Do you accelerate the students so that they can be ready for algebra 2 as freshmen? Do you spend the extra time doing all the cool stuff that no one else has time to do because they are worried about pacing guides and benchmarks? We've decided to go ahead and accelerate them. I'm still a bit unsettled about it, though. Is it really that important for an 8th grader to complete geometry so she can take algebra 2 in 9th grade? The kid is on pace to take calculus as a junior. Is that better? At this point, I don't know. In the era of "the TEST", it seems that as long as I have the data to back up what I am doing, it doesn't matter what we choose. My kids have the test scores, but I am not convinced that what I am doing is the right thing.
I am definitely in unchartered waters. As a high school teacher, I was simply one of many. My last year there, we had a pacing guide and all common assessments. It was pretty lock step and I was miserable--loved the staff and the students--but hated the system. Now I have a bunch of autonomy because I can keep the powers that be off my back with some good scores, but I am not sure what direction to go.
Last year, the decision was a bit easier because I got to hand pick the students who would move into the geometry class. I taught both advanced 7th grade classes so I knew they were ready. This year--not so much. I have two classes made up of kids from two different teachers. Some are ready to be accelerated and others look like they are going to need to spend some serious time with the algebra. My question for you all is this: how do you plan for these classes? Half of my students have already been through algebra, a quarter of them have been exposed to it and the rest look like they may not know what a variable is. I've never been here before, so I don't know what to expect. If you've ever considered commenting on a post here, now's the time. Hit me up.
The thought was, "Rather than ship the really smart kids to high school to take the geometry class, we'll just bring the high school teacher to them."
I didn't mind this idea. In fact, it quickly began to grow on me. I was teaching precalc, algebra 2 and algebra 1 at the high school and figured the change might do me some good. The tough part was that I had no idea what to expect. I was going from 55 minute periods to 94 minute daily blocks.
What the heck am I going to do with a group of middle schoolers for 94 minutes?
So after many discussions with my principal, we decided that since the 94 minute block was intended to allow for grade level instruction as well as time for intervention, I'd just use my extra time for enrichment. But what do you do to enrich them? Do you accelerate the students so that they can be ready for algebra 2 as freshmen? Do you spend the extra time doing all the cool stuff that no one else has time to do because they are worried about pacing guides and benchmarks? We've decided to go ahead and accelerate them. I'm still a bit unsettled about it, though. Is it really that important for an 8th grader to complete geometry so she can take algebra 2 in 9th grade? The kid is on pace to take calculus as a junior. Is that better? At this point, I don't know. In the era of "the TEST", it seems that as long as I have the data to back up what I am doing, it doesn't matter what we choose. My kids have the test scores, but I am not convinced that what I am doing is the right thing.
I am definitely in unchartered waters. As a high school teacher, I was simply one of many. My last year there, we had a pacing guide and all common assessments. It was pretty lock step and I was miserable--loved the staff and the students--but hated the system. Now I have a bunch of autonomy because I can keep the powers that be off my back with some good scores, but I am not sure what direction to go.
Last year, the decision was a bit easier because I got to hand pick the students who would move into the geometry class. I taught both advanced 7th grade classes so I knew they were ready. This year--not so much. I have two classes made up of kids from two different teachers. Some are ready to be accelerated and others look like they are going to need to spend some serious time with the algebra. My question for you all is this: how do you plan for these classes? Half of my students have already been through algebra, a quarter of them have been exposed to it and the rest look like they may not know what a variable is. I've never been here before, so I don't know what to expect. If you've ever considered commenting on a post here, now's the time. Hit me up.
Whatever It Takes
Our campus has been having some great conversations centered on developing tiered lessons that allow for differentiation depending not only on ability level but on learning modality. How can we reach a student at their appropriate cognitive level while respecting whether they are an auditory, visual or kinesthetic learner? Now, I am no cognitive scientist nor am I an expert at developing curriculum. But I do know that meeting kids where they are is a good idea. How we implement that is a different story. Haven't figured that one out.
Last year I had a student who would have bounced off the walls if I didn't keep him engaged. Getting this kid to do homework was nearly impossible because it interfered with his gaming time.
"Look over your notes tonight," I'd say.
"Yeah, right," he'd think. "What do I want to do that for? I gotta date with Xbox Live!"
But then I started a channel on blip.tv where I would upload any mathcasts I created so students would have access to them from home. Dang it if this kid didn't subscribe to the RSS feed. It hit me when one day after a test, he told me:
"Hey Mr. Cox, that test was easy. I watched the examples on my PSP last night."
Do these digital natives process information differently? Is this a new modality?
Last year I had a student who would have bounced off the walls if I didn't keep him engaged. Getting this kid to do homework was nearly impossible because it interfered with his gaming time.
"Look over your notes tonight," I'd say.
"Yeah, right," he'd think. "What do I want to do that for? I gotta date with Xbox Live!"
But then I started a channel on blip.tv where I would upload any mathcasts I created so students would have access to them from home. Dang it if this kid didn't subscribe to the RSS feed. It hit me when one day after a test, he told me:
"Hey Mr. Cox, that test was easy. I watched the examples on my PSP last night."
Do these digital natives process information differently? Is this a new modality?
Wednesday, August 19, 2009
Is This What I Do or Is It Who I Am?
I really have to hand it to you people. Man, some of you guys kept the great conversations going from the time school let out 'till the opening bell of this school year. I know some of you actually still start in September, but great conversaions nonetheless.
I just couldn't do it. I meant to, but I couldn't. Sure, I had a bunch of ideas of what I wanted to work on during the summer but they all got trumped by four little boys who kept wanting to wrestle. How can you pass up on getting dog piled by these guys?

So needless to say, I didn't get much school stuff done. I kind of felt bad about it; especially when I thought of all the teachers out there who put in 60+ hours per week and hammer out curriculum over the summer. I see the Tweets and blog posts--you people are amazing. The question has come to mind: Is This What I Do or Is It Who I Am? Is teaching my job, or is it my essence? I struggle with that all the time. I struggle because I realize that everytime I say yes to an extra hour of planning, that is one less hour I have to spend with my wife and boys. I want to be one of those teachers who can put in an extra four hours per day planning great lessons, but I simply can't. Does that mean someone is gonna pull my teacher card? Hope not. This is a great job. And the one thing I know for sure is that the better dad I am, the better teacher I become.
I just couldn't do it. I meant to, but I couldn't. Sure, I had a bunch of ideas of what I wanted to work on during the summer but they all got trumped by four little boys who kept wanting to wrestle. How can you pass up on getting dog piled by these guys?

So needless to say, I didn't get much school stuff done. I kind of felt bad about it; especially when I thought of all the teachers out there who put in 60+ hours per week and hammer out curriculum over the summer. I see the Tweets and blog posts--you people are amazing. The question has come to mind: Is This What I Do or Is It Who I Am? Is teaching my job, or is it my essence? I struggle with that all the time. I struggle because I realize that everytime I say yes to an extra hour of planning, that is one less hour I have to spend with my wife and boys. I want to be one of those teachers who can put in an extra four hours per day planning great lessons, but I simply can't. Does that mean someone is gonna pull my teacher card? Hope not. This is a great job. And the one thing I know for sure is that the better dad I am, the better teacher I become.
Friday, May 29, 2009
Hom-asse-ferentiation
All the new schools come with cafegymatoriums so I figure I'll go with a 3-in-1 post.
For 12 years I had assigned it but it always bugged me that we would spend 15+ minutes the next day going over something that many of the students didn't complete. And if they did bring it in, how did I know if it was actually their work? Now that I have children of my own in school, I am even more bothered by the amount of busywork that imposes itself on family time.
My question isn't regarding the validity of homework. My question revolves around the idea of how to make homework matter. How do we make it meaningful to our students? Can we tie it to assessment and/or differentiate it so that kids can work on what they need at any given point in time? And further, can homework become part of a meaningful dialogue between teacher and student rather than a box to be checked on the daily "to do" list?
Quiz, Quiz, Test. Quiz, Quiz, Test. Quiz, Quiz, Test.
Isn't that how the pattern goes? Followed that one too. But again, over the past few years, my view of assessment has changed. When do we assess? How often? How many times should a student have to show us he can do something? How many different ways should he have to show it? Multiple choice or free response? Where does writing come into play?
For the past three years, we have been dealing with pacing guides and benchmarks due to the fact that my district is in program improvement. I am in favor of it. Pacing guides and benchmarks have allowed us to begin with the end in mind, check for understanding along the way and then find ways to intervene with students who are struggling to grasp the concepts/skills. However, I have noticed that teachers have a tendency to become very procedure oriented and lose sight of all the great thinking that can be provoked in a math classroom. I don't blame this on pacing and benchmarks any more than I blame bad lessons on the tools being used in the classroom. It has become obvious that the textbook pacing isn't the way we want to go, so we have started to teach one standard at a time. But I think that many of our standards need to be deconstructed even more in order to ensure that when we assess, we get a grip on where a student is really struggling. For example, in California, Algebra Standard 15.0 deals with mixture, rate and work problems. It isn't enough to say that a kid is struggling with 15.0, we need to be a bit more specific in order to fix the problem. I know that Dan has done a nice job of explaining the need to break the curriculum down into skills and he has a great assessment plan. The part we have struggled with is what to do in between the initial assessment and the re-assessment(s). Which leads us to...
Is it enough to throw some review problems up on the board for warmups and call it "intervention?" Do we give students different assignments based on their need -- and when we give these assignments, how do we grade them? How much weight do they carry in relation to the final grade? Can I actually have 30 kids working on 30 different things? If so, does that mean that I have to come up with 30 different assignments for each skill I want to remediate? My head hurts just thinking about it.
Until recently.
Why can't we tie them all together? Why can't homework/classwork be prescribed based on the results of an initial assessment becomming a prerequesite for the re-assessment; a key to unlock the assessment box. A student can be placed into one of two paths: the road to proficiency or the road to advanced status. Once a student reaches proficiency in a certain standard/skill, he earns a B. He then has the choice to move towards advanced status in that skill (for an A) or work towards proficiency in another skill. If he never moves onto the advanced path, the score for that skill remains a B. I am not sure if we should go with a 1-5 grading system or attach a percentage to the rubric score. (ie. 5 = 90%, 4 = 85%, 3 = 75%, 2 = 65%, 1 = 50%)
Over the past month, I have had some release days and have come up with a template. The challenging part has been to decide which "tasks" a student must complete before being allowed to re-assess. These tasks are very minimal in that they merely show what I would like a student be able to show before he is allowed to re-assess. Could a student take these tasks and "create" their own problems based on the template, or would the teacher need to be more hands on in helping direct the student? Are there skills I am missing? Are there ways to demonstrate the skill that I am leaving out? How can this be adapted for student interest and/or modality? And most importantly: does this idea stand a chance? I would really appreciate any feedback that I can get on this.
Note: Our math classes are in 94 minute daily blocks, so time for intervention/enrichment is built in. We will go with a sort of 60-30 model next year where we do regular instruction for the first 60 minutes and leave the last 30 minutes for students to work on their choice of previous skills.
The proficiency tasks for each skill will be followed by the student doing an exemplar. My working definition of "exemplar" is a problem that exemplifies the given skill worked by the student with written and/or verbal explanation of the process used. I have found these to be very good authentic assessments. The student has the option to do this via paper and pencil or mathcast.
Homework
For 12 years I had assigned it but it always bugged me that we would spend 15+ minutes the next day going over something that many of the students didn't complete. And if they did bring it in, how did I know if it was actually their work? Now that I have children of my own in school, I am even more bothered by the amount of busywork that imposes itself on family time.
My question isn't regarding the validity of homework. My question revolves around the idea of how to make homework matter. How do we make it meaningful to our students? Can we tie it to assessment and/or differentiate it so that kids can work on what they need at any given point in time? And further, can homework become part of a meaningful dialogue between teacher and student rather than a box to be checked on the daily "to do" list?
Assessment
Quiz, Quiz, Test. Quiz, Quiz, Test. Quiz, Quiz, Test.
Isn't that how the pattern goes? Followed that one too. But again, over the past few years, my view of assessment has changed. When do we assess? How often? How many times should a student have to show us he can do something? How many different ways should he have to show it? Multiple choice or free response? Where does writing come into play?
For the past three years, we have been dealing with pacing guides and benchmarks due to the fact that my district is in program improvement. I am in favor of it. Pacing guides and benchmarks have allowed us to begin with the end in mind, check for understanding along the way and then find ways to intervene with students who are struggling to grasp the concepts/skills. However, I have noticed that teachers have a tendency to become very procedure oriented and lose sight of all the great thinking that can be provoked in a math classroom. I don't blame this on pacing and benchmarks any more than I blame bad lessons on the tools being used in the classroom. It has become obvious that the textbook pacing isn't the way we want to go, so we have started to teach one standard at a time. But I think that many of our standards need to be deconstructed even more in order to ensure that when we assess, we get a grip on where a student is really struggling. For example, in California, Algebra Standard 15.0 deals with mixture, rate and work problems. It isn't enough to say that a kid is struggling with 15.0, we need to be a bit more specific in order to fix the problem. I know that Dan has done a nice job of explaining the need to break the curriculum down into skills and he has a great assessment plan. The part we have struggled with is what to do in between the initial assessment and the re-assessment(s). Which leads us to...
Differentiation
Is it enough to throw some review problems up on the board for warmups and call it "intervention?" Do we give students different assignments based on their need -- and when we give these assignments, how do we grade them? How much weight do they carry in relation to the final grade? Can I actually have 30 kids working on 30 different things? If so, does that mean that I have to come up with 30 different assignments for each skill I want to remediate? My head hurts just thinking about it.
Until recently.
Why can't we tie them all together? Why can't homework/classwork be prescribed based on the results of an initial assessment becomming a prerequesite for the re-assessment; a key to unlock the assessment box. A student can be placed into one of two paths: the road to proficiency or the road to advanced status. Once a student reaches proficiency in a certain standard/skill, he earns a B. He then has the choice to move towards advanced status in that skill (for an A) or work towards proficiency in another skill. If he never moves onto the advanced path, the score for that skill remains a B. I am not sure if we should go with a 1-5 grading system or attach a percentage to the rubric score. (ie. 5 = 90%, 4 = 85%, 3 = 75%, 2 = 65%, 1 = 50%)
Over the past month, I have had some release days and have come up with a template. The challenging part has been to decide which "tasks" a student must complete before being allowed to re-assess. These tasks are very minimal in that they merely show what I would like a student be able to show before he is allowed to re-assess. Could a student take these tasks and "create" their own problems based on the template, or would the teacher need to be more hands on in helping direct the student? Are there skills I am missing? Are there ways to demonstrate the skill that I am leaving out? How can this be adapted for student interest and/or modality? And most importantly: does this idea stand a chance? I would really appreciate any feedback that I can get on this.
Note: Our math classes are in 94 minute daily blocks, so time for intervention/enrichment is built in. We will go with a sort of 60-30 model next year where we do regular instruction for the first 60 minutes and leave the last 30 minutes for students to work on their choice of previous skills.
The proficiency tasks for each skill will be followed by the student doing an exemplar. My working definition of "exemplar" is a problem that exemplifies the given skill worked by the student with written and/or verbal explanation of the process used. I have found these to be very good authentic assessments. The student has the option to do this via paper and pencil or mathcast.
Friday, May 22, 2009
Tuesday, May 19, 2009
For All the Marbles...
Final exam. One question.
How Tall Is It?
"Show me two different ways you could figure the height of the building."
"That's easy, Mr. Cox. Measure a brick and count the number of rows."
"Alright, make it three, smart guy."
Friday, May 15, 2009
Are Two Ways Better Than One?
Graphing parabolas is much easier when we can zero in on "key points." The CPM Algebra 2 curriculum was great about dealing with "parent graphs" and then showing students the process for translating and stretching these parents. It is easy to get away from this as we have other skills that we need to teach. But this year, I have really focused on having my students get really comfortable with y = x2 and then recognizing that all parabolas are really just different perspectives of this parent graph. Zoom out and the parabola get skinnier; zoom in and it gets fatter. If you know the vertex and stretch factor, then you are ready to do some graphing; this works for vertex or standard form.
One of the more interesting developments during this unit has been my students recognizing that the rate of change in a parabola has a rate of change. They are wrestling with the concepts behind derivatives and I want to keep them in that fight as long as possible. I usually have my students graph five points and I have always had them relate those five points back to the vertex. However, with the way they are handling rate of change, I need to rethink my process.
 Simply use the stretch factor to adjust the relationships:
Simply use the stretch factor to adjust the relationships: This year I have given them choice on this, but it has caused a few kids confusion as they end up with a hybrid process. Next year? Not so sure.
This year I have given them choice on this, but it has caused a few kids confusion as they end up with a hybrid process. Next year? Not so sure.
One of the more interesting developments during this unit has been my students recognizing that the rate of change in a parabola has a rate of change. They are wrestling with the concepts behind derivatives and I want to keep them in that fight as long as possible. I usually have my students graph five points and I have always had them relate those five points back to the vertex. However, with the way they are handling rate of change, I need to rethink my process.
 Simply use the stretch factor to adjust the relationships:
Simply use the stretch factor to adjust the relationships: This year I have given them choice on this, but it has caused a few kids confusion as they end up with a hybrid process. Next year? Not so sure.
This year I have given them choice on this, but it has caused a few kids confusion as they end up with a hybrid process. Next year? Not so sure.
Thursday, May 14, 2009
Ya Think?
Teacher: "What do you think about...?"
Student: "I don't know." Translation: What do you want me to think?
A recent post by Jason Dyer regarding the findings of Piaget being re- interpreted by James McGarrigle and Margaret Donaldson has me thinking about how often I give off context clues without even thinking about it.
*nodding head, smiling* "Do you understand now?"
*raising hand* "Raise your hand if you get it."
*squinting with furrowed brow, head cocked to the side* "Can you explain how you got that answer?"
And more importantly, how I perpetuate the very thing that I beleive is wrong with education.
They cue in fast...really fast. Mine cue in faster than others 'cause I got the smart ones. But you know what, they don't think better than the others, they just figure out what the teacher wants to hear faster and at a higher accuracy rate. They play "school" better. The ones who are the real thinkers are the smart kids we call lazy. Yeah, that one-- the kid who doesn't turn stuff in or do homework but crushes every test.
I am starting to think it's not his fault. Maybe, just maybe, he's just not interested in me giving him answers to questions he doesn't care to ask.
Student: "I don't know." Translation: What do you want me to think?
A recent post by Jason Dyer regarding the findings of Piaget being re- interpreted by James McGarrigle and Margaret Donaldson has me thinking about how often I give off context clues without even thinking about it.
*nodding head, smiling* "Do you understand now?"
*raising hand* "Raise your hand if you get it."
*squinting with furrowed brow, head cocked to the side* "Can you explain how you got that answer?"
And more importantly, how I perpetuate the very thing that I beleive is wrong with education.
They cue in fast...really fast. Mine cue in faster than others 'cause I got the smart ones. But you know what, they don't think better than the others, they just figure out what the teacher wants to hear faster and at a higher accuracy rate. They play "school" better. The ones who are the real thinkers are the smart kids we call lazy. Yeah, that one-- the kid who doesn't turn stuff in or do homework but crushes every test.
I am starting to think it's not his fault. Maybe, just maybe, he's just not interested in me giving him answers to questions he doesn't care to ask.
Tuesday, May 12, 2009
Stretch Factor
What does a normal parabola look like again?

And what about one with a stretch factor of 7?

And how about 1/10?

Nice job folks.
Now get out some paper and get to work!
And quit smiling...math ain't that fun.

And what about one with a stretch factor of 7?

And how about 1/10?

Nice job folks.
Now get out some paper and get to work!
And quit smiling...math ain't that fun.
Monday, May 11, 2009
Chandler Saves the Day
You ever have a lesson that you thought was going to go pretty well only to have it fall flat? Yeah, that happened today.
My 7th graders have been going over quadratics for the past couple of weeks. I have been out quite a bit on school business, so the progress has been slow, but very rewarding. Last week, students discovered that if you change the value of "a", it has an effect on how fast the parabola grows. I then had them graph a bunch of parabolas whose line of symmetry was the y-axis only to have a student ask,
"Can we move the parabola left or right?"
"Well since you asked..." So I did what any responsible teacher would...I had them graph a bunch of parabolas whose vertex sat on the x-axis which led to the next question,
"Can we move them up/down and left/right?"
So Friday, we are graphing parabolas in the form y =a(x-h)^2 +k and they are getting it. This is stuff I couldn't do until Algebra II with my high school students and these 7th graders are just crushing everything I throw at them. I would even give them a vertex and a second point and they were giving me an equation because they figured the stretch factor using the second point. Things are looking good and I am thinking:
Man this is just toooo easy...
Yeah, I know, pride comes before the fall. Which is what started to happen today. I have had a planning block. Now that we have graphed a bunch of parabolas in vertex form, where do I go from there? Do I start dealing with standard form? Do I show them how to expand (x-h)^2 in order to arrive at standard form? I am still not sure what the ideal path would be. But being the "try anything once" kind of guy I am, I figured that since I have already had them:
...then I would focus in on what was necessary to graph a parabola: vertex and stretch factor. If they could identify the vertex and a stretch factor, they can graph anything, right? So today I wanted them to graph a bunch of parabolas in standard form, look for the line of symmetry and recognize the relationship between a,b and the line of symmetry. I didn't expect them to necessarily "discover" that the line of symmetry is x = -b/(2a), but I figured that if we graphed enough of them, we might start to notice some patterns. Once we have the line of symmetry down, then we could start looking at x intercepts which would lead us to factoring and completing the square as well as quadratic formula. (If my sequencing on this is bad, please save me from myself. )
This is where it started to go bad. GeoGebra is a great program, but it doesn't save a weak lesson. Kids were all over the place with their parabolas and we were getting lines of symmetry like x=.7923496, which wasn't going to help at all. I was about to put us all out of our misery and jump ship when Chandler says, "Mr. Cox come here, I think I found something."
She had about 10 parabolas that all had the same line of symmetry. She was making adjustments to the a and b values and recognized that the c value had no effect on the symmetry. So rather than aborting the mission, we just changed course.
"How about choosing a line of symmetry and keeping the vertex on that line?"
They got right to it. Tomorrow they are going to come to class with five different a,b,c values and the corresponding line of symmetry. We will see where it goes.
Note to the reader: Quadratics are not a 7th grade standard and these kids will go through it on a deeper level as 8th graders. So, I am not worried about "finishing" this with them. I have the flexibility to let concepts marinade for a while. Usually, I would have just followed the pacing of the book, but I have become very dissatisfied with that. I am pretty sure that I want to continue from linear relations right into quadratic relations and that graphing is a good gateway to all the other skills that go along with quadratics. I am just not sure how one skill will best lead into another. Any suggestions?
Note to self: Quit gettin' ahead of yourself and be sure to see the lesson through the eyes of a student rather than your own.
Oh yeah, and thank Chandler.
My 7th graders have been going over quadratics for the past couple of weeks. I have been out quite a bit on school business, so the progress has been slow, but very rewarding. Last week, students discovered that if you change the value of "a", it has an effect on how fast the parabola grows. I then had them graph a bunch of parabolas whose line of symmetry was the y-axis only to have a student ask,
"Can we move the parabola left or right?"
"Well since you asked..." So I did what any responsible teacher would...I had them graph a bunch of parabolas whose vertex sat on the x-axis which led to the next question,
"Can we move them up/down and left/right?"
So Friday, we are graphing parabolas in the form y =a(x-h)^2 +k and they are getting it. This is stuff I couldn't do until Algebra II with my high school students and these 7th graders are just crushing everything I throw at them. I would even give them a vertex and a second point and they were giving me an equation because they figured the stretch factor using the second point. Things are looking good and I am thinking:
Man this is just toooo easy...
Yeah, I know, pride comes before the fall. Which is what started to happen today. I have had a planning block. Now that we have graphed a bunch of parabolas in vertex form, where do I go from there? Do I start dealing with standard form? Do I show them how to expand (x-h)^2 in order to arrive at standard form? I am still not sure what the ideal path would be. But being the "try anything once" kind of guy I am, I figured that since I have already had them:
- Graph quadratics organically (area vs. radius; area vs. side length)
- Graph quadratics with a not equal to 1.
- Graph quadratics with vertex on y axis.
- Graph quadratics with vertex on x axis.
- Graph quadratics in the form y = a(x-h)^2 +k
...then I would focus in on what was necessary to graph a parabola: vertex and stretch factor. If they could identify the vertex and a stretch factor, they can graph anything, right? So today I wanted them to graph a bunch of parabolas in standard form, look for the line of symmetry and recognize the relationship between a,b and the line of symmetry. I didn't expect them to necessarily "discover" that the line of symmetry is x = -b/(2a), but I figured that if we graphed enough of them, we might start to notice some patterns. Once we have the line of symmetry down, then we could start looking at x intercepts which would lead us to factoring and completing the square as well as quadratic formula. (If my sequencing on this is bad, please save me from myself. )
This is where it started to go bad. GeoGebra is a great program, but it doesn't save a weak lesson. Kids were all over the place with their parabolas and we were getting lines of symmetry like x=.7923496, which wasn't going to help at all. I was about to put us all out of our misery and jump ship when Chandler says, "Mr. Cox come here, I think I found something."
She had about 10 parabolas that all had the same line of symmetry. She was making adjustments to the a and b values and recognized that the c value had no effect on the symmetry. So rather than aborting the mission, we just changed course.
"How about choosing a line of symmetry and keeping the vertex on that line?"
They got right to it. Tomorrow they are going to come to class with five different a,b,c values and the corresponding line of symmetry. We will see where it goes.
Note to the reader: Quadratics are not a 7th grade standard and these kids will go through it on a deeper level as 8th graders. So, I am not worried about "finishing" this with them. I have the flexibility to let concepts marinade for a while. Usually, I would have just followed the pacing of the book, but I have become very dissatisfied with that. I am pretty sure that I want to continue from linear relations right into quadratic relations and that graphing is a good gateway to all the other skills that go along with quadratics. I am just not sure how one skill will best lead into another. Any suggestions?
Note to self: Quit gettin' ahead of yourself and be sure to see the lesson through the eyes of a student rather than your own.
Oh yeah, and thank Chandler.
Monday, May 4, 2009
Upgraded to Pandemic
At least in my own head. No, I can't shut it off! Not sure I would want to even if I could.
I am getting gas the other day and this shot is screaming at me:
So today, I put the slide up and the kids immediately start talking about slope. I like that they thought slope, but slope isn't really going to do much when it comes to fences. So I asked them:
"What would you want to know if you had to build the fence?"
They caught on pretty quickly that one would want to know the length of each board.
"Alright, then tell me the length of each board."
"But, Mr. Cox, we don't have enough information."
"What do you want to know?"
"We need to know how long the shortest board is."
Done.

"Alright, now tell me how long each board is."
"We can't. We need more information."
So I had them discuss with their groups what information they had to have in order to figure out how long each board was. Once they had an exhaustive list, they were to write it on their group's easel. We quickly came up with the following:
So do we need the next board, or will any board do? We eventually settled on any other board.
It didn't take long before students had listed all the board lengths. Many used the rate of change and then added the increase to each board to find the length of the next. But it did't take much prodding for them to realize that having an equation would be nice. We came up with y = 2.5x + 36 fairly quickly. The interesting discussion came about when I asked what x represented.
"X is the number of boards."
"Okay, so go up to the board and point to board #1."
Which board do you think they pointed to? (You guessed it, the one labeled 36". )
"So, plug 1 into your equation and check it out. Tell me if your equation works."
You would have thought that I asked them to stand in the corner of a round room. But once the "but this equation haa-aas to work" wore off. They realized that it wasn't the equation's fault. It was how they defined x. Board 0 is important because we aren't actually counting boards, we are counting the number of increases.
Reflection: I think that the lesson went really well, but it was very telling how many students wanted to impress with their knowledge of the vocabulary as opposed to just looking at the problem and asking the obvious questions. They were trying to be mathematicians rather than someone who just needs to build a fence. Next year I want to do a better job of introducing concepts a bit more organically as opposed to "here are the rules, here are some examples, let's get to it." Students are much more engaged when the information is given a little at a time. It keeps them from answer chasing and allows them to think a little. It may take a bit longer to deliver the lesson, but the benefit of having kids think about the math is priceless.
Questions: What else could I have done with this image?
I am getting gas the other day and this shot is screaming at me:

So today, I put the slide up and the kids immediately start talking about slope. I like that they thought slope, but slope isn't really going to do much when it comes to fences. So I asked them:
"What would you want to know if you had to build the fence?"
They caught on pretty quickly that one would want to know the length of each board.
"Alright, then tell me the length of each board."
"But, Mr. Cox, we don't have enough information."
"What do you want to know?"
"We need to know how long the shortest board is."
Done.

"Alright, now tell me how long each board is."
"We can't. We need more information."
So I had them discuss with their groups what information they had to have in order to figure out how long each board was. Once they had an exhaustive list, they were to write it on their group's easel. We quickly came up with the following:
- The length of the next board.
- The length of one more board.
- The width of each board.
So do we need the next board, or will any board do? We eventually settled on any other board.
It didn't take long before students had listed all the board lengths. Many used the rate of change and then added the increase to each board to find the length of the next. But it did't take much prodding for them to realize that having an equation would be nice. We came up with y = 2.5x + 36 fairly quickly. The interesting discussion came about when I asked what x represented.
"X is the number of boards."
"Okay, so go up to the board and point to board #1."
Which board do you think they pointed to? (You guessed it, the one labeled 36". )
"So, plug 1 into your equation and check it out. Tell me if your equation works."
You would have thought that I asked them to stand in the corner of a round room. But once the "but this equation haa-aas to work" wore off. They realized that it wasn't the equation's fault. It was how they defined x. Board 0 is important because we aren't actually counting boards, we are counting the number of increases.
Reflection: I think that the lesson went really well, but it was very telling how many students wanted to impress with their knowledge of the vocabulary as opposed to just looking at the problem and asking the obvious questions. They were trying to be mathematicians rather than someone who just needs to build a fence. Next year I want to do a better job of introducing concepts a bit more organically as opposed to "here are the rules, here are some examples, let's get to it." Students are much more engaged when the information is given a little at a time. It keeps them from answer chasing and allows them to think a little. It may take a bit longer to deliver the lesson, but the benefit of having kids think about the math is priceless.
Questions: What else could I have done with this image?
Friday, May 1, 2009
Intro to Quadratics: 7th Grade Style
Can I just say that I love middle school kids. I mean, sometimes keeping them on the same page is like trying to herd a bunch of cats, but I love them. Now that testing is over, it is time to start preparing my 7th graders for the wonderful world of quadratics. We have been doing a bunch of activities on linear relationships and the results have been pretty good. My kids have a pretty firm grasp of the following:
They like lines; they are comfortable with lines. It is time to take them out of their comfort zone. So here is how it went down:
We had already done some activities on linear relationships like:
The latest installment was to have them bring in a few circular items and then find the relationship between radius vs. circumference. This led quite nicely into, 'Well, since you have some circles here, you may as well calculate the areas too. Graph those compared to the radius and see what you get."
It was interesting to see how many kids tried to force it into a linear relationship.
Angel recognized that "choosing a bunch of circles with around the same radius doesn't tell us much, huh, Mr. Cox."
"Nope, next time we may want to expand our sample space."
Regardless, by the end of the activity, they understood that sometimes we have relationships that are "curved" or "non-linear." Fareen recognized that we get a "half of a parabola."
So from there we do some work with the side length vs. area of a square. Hey, we may as well start at the beginning, right? But it was the simplicity of the exercise that produced the magic that I never saw in 10 years of teaching high school kids the same thing.
"Hey, Mr. Cox, it isn't a line because the slopes don't stay the same."
"Yeah, so what?"
"Well the areas increase by 3, then 5 then 7. But the increases all increase by 2."
"Okay, so what does that mean?"
"The rate of change has a rate of change."
At this point I get goosebumps.
This is when Abel, asks: "What will happen if we cube x? What happens to the rate of change then?"
Couldn't pass this one up, so we drew up a chart and did it. The kids concluded that for a cubic: the rate of change of the rate of change has a rate of change. Oh, and the number of times we have to check the rate of change tells us what the exponent is.
Moral of the story: Don't assume that your lesson objective is the right one.
or, Sometimes it is better to follow the herd of cats.
- Slope and rate of change mean the same thing.
- If the rate of change remains the same, then we have a line.
- The initial condition is the y intercept.
- If the initial condition is 0, then we have a direct variation.
They like lines; they are comfortable with lines. It is time to take them out of their comfort zone. So here is how it went down:
We had already done some activities on linear relationships like:
- Farenheit vs. Celcius
- cm vs. inches
- km vs. miles
- start height vs. rebound height for a bouncing ball on concrete between 75 and 80 degrees with no wind resistance. (Alright, we didn't control the experiment that much, but they still saw that the ball rebounded to about 70% the original height. Daniel learned that baseballs don't bounce very high when you drop them from 1 meter and the seams mess up the bounce.)
The latest installment was to have them bring in a few circular items and then find the relationship between radius vs. circumference. This led quite nicely into, 'Well, since you have some circles here, you may as well calculate the areas too. Graph those compared to the radius and see what you get."
It was interesting to see how many kids tried to force it into a linear relationship.
Angel recognized that "choosing a bunch of circles with around the same radius doesn't tell us much, huh, Mr. Cox."
"Nope, next time we may want to expand our sample space."
Regardless, by the end of the activity, they understood that sometimes we have relationships that are "curved" or "non-linear." Fareen recognized that we get a "half of a parabola."
So from there we do some work with the side length vs. area of a square. Hey, we may as well start at the beginning, right? But it was the simplicity of the exercise that produced the magic that I never saw in 10 years of teaching high school kids the same thing.
"Hey, Mr. Cox, it isn't a line because the slopes don't stay the same."
"Yeah, so what?"
"Well the areas increase by 3, then 5 then 7. But the increases all increase by 2."
"Okay, so what does that mean?"
"The rate of change has a rate of change."

At this point I get goosebumps.
This is when Abel, asks: "What will happen if we cube x? What happens to the rate of change then?"
Couldn't pass this one up, so we drew up a chart and did it. The kids concluded that for a cubic: the rate of change of the rate of change has a rate of change. Oh, and the number of times we have to check the rate of change tells us what the exponent is.

Moral of the story: Don't assume that your lesson objective is the right one.
or, Sometimes it is better to follow the herd of cats.
Tuesday, April 28, 2009
No, Seriously... I Need Your Help
Alright, my head is about to explode. For the next two days I'll be sitting here in a room all alone trying to figure out how the heck we are supposed to bridge this gap. I have all the tools ready to go(computers, legal pads, pens, state framework,etc.). And all of a sudden it hits me. The rules of math have come about because they were necessary. For example, Natural numbers work until you try to subtract. Then you have to have integers. Integers are fine until you divide, which leads to Rational numbers. The Rational numbers break down when you try to find the side length of a square with an area of 15. Take the kids on this tour and we get to say: "Okay class, we have just discovered the Real Number system."
We have exponents and scientific notation because it get really tedious to multiply (5,000,000,000)(8,000,000) by hand. We introduce the symbols and variables because we don't want to have to work out every single case for every single situation. We generalize because mathematicians are inherently lazy. We truly find the shortest distance between two points. Kids are inherently lazy; they know the shortest distance between homework and their XBox. Hey, we have someting in common. How do we expolit that commonality in order to have kids "discover" algebra for themselves? How do we scaffold our entire curriculum, so that kids move from the Natural Numbers to Projectile Motion in such a way that they actually see how there is a need for it?
I realize that I am probably not saying anything you all haven't already discovered for yourselves. But, before I go and reinvent this wheel, I would like to know what you have all been doing to get this Algebra bus rollin'.
We have exponents and scientific notation because it get really tedious to multiply (5,000,000,000)(8,000,000) by hand. We introduce the symbols and variables because we don't want to have to work out every single case for every single situation. We generalize because mathematicians are inherently lazy. We truly find the shortest distance between two points. Kids are inherently lazy; they know the shortest distance between homework and their XBox. Hey, we have someting in common. How do we expolit that commonality in order to have kids "discover" algebra for themselves? How do we scaffold our entire curriculum, so that kids move from the Natural Numbers to Projectile Motion in such a way that they actually see how there is a need for it?
I realize that I am probably not saying anything you all haven't already discovered for yourselves. But, before I go and reinvent this wheel, I would like to know what you have all been doing to get this Algebra bus rollin'.
Friday, April 24, 2009
Dear Dan,
You are really starting to make me angry. I was content to just do my job, help as many kids as I could, do some extra stuff to help them make it connect to their reality. And then at 4:00pm shut it down, go home, kiss my wife, play with the kids, have a nice dinner, watch a little TV and go to bed. But no! You just had to start in with all this "using pictures to help kids learn math" stuff. You couldn't leave well enough alone. When I couldn't get Graphing Stories to work, you couldn't just say "sorry dude, I am not sure why those chapters won't play. Better luck next time"... no you had to send me a copy and not even take the reimbursement I offered. Who do you think you are?
Man I can't even go to Target with my family without trying to take a picture of something. You know how disruptive that is? You know how hard it is to hold the baby, push the cart and snap a pic at the same time? I am looking into having an extra arm grafted onto my torso. You think my insurance will cover that? Nooooo! And it is all because of YOU!
The worst part is that I have these video cameras lying around my classroom and a blue screen in the library so I had to skip lunch the other day and take some footage that has resulted in some stills like these:
I mean, look at that. How can they not see that the ball is accelerating as it falls? I don't want that. I want them to depend on me to tell them that gravity is an acceleration.
[caption id="attachment_134" align="aligncenter" width="300" caption="I'm not mad at you for this one, I actually think it's pretty cool. "] [/caption]
[/caption]
What's even worse, is I have all this raw video footage and I have no friggin' idea what to do with it. What am I supposed to do, have students graph the height of the ball vs. time and realize that there are some relationships that aren't linear?
My students are even getting into the taping. They look so cute and happy throwing the ball back and forth, but little do they know that one day this concept of math actually helping them to interpret the world around them can consume them. What's next? Are we going to start treating mathematics like a humanity and sit around discussing it as if it were a piece of literature or work or art? Don't you know that math is only supposed to be important 8:20-2:55 in Room 405 from September to June? Don't you know that math is supposed to be a set of rules that we force our kids to memorize until April 22 and then they aren't supposed to think about it again? Get with the program, will ya?
And no textbook? C'mon, man! What are you thinking? Those things were all written by people who really care about making math matter to our children. Don't you know that the more a student sits in front of a textbook, the more they learn? I saw some research done by an independent agency Houghton, McGraw, Holt and Littell that says students can actually teach themselves with these things.
In closing, you have got it all wrong. Kids want to have subjects forced upon them. They want to be told the rules, they want to mindlessly copy exactly what the teacher says and does and they especially want to ask questions like, "I don't get it."
Inquiry? Yeah, right!
Sincerely,
David
p.s. Can I make a cameo in Graphing Stories vol. 2?
p.p.s Can you all help me package this up into a series of lessons?
Man I can't even go to Target with my family without trying to take a picture of something. You know how disruptive that is? You know how hard it is to hold the baby, push the cart and snap a pic at the same time? I am looking into having an extra arm grafted onto my torso. You think my insurance will cover that? Nooooo! And it is all because of YOU!
The worst part is that I have these video cameras lying around my classroom and a blue screen in the library so I had to skip lunch the other day and take some footage that has resulted in some stills like these:



I mean, look at that. How can they not see that the ball is accelerating as it falls? I don't want that. I want them to depend on me to tell them that gravity is an acceleration.
[caption id="attachment_134" align="aligncenter" width="300" caption="I'm not mad at you for this one, I actually think it's pretty cool. "]
 [/caption]
[/caption]What's even worse, is I have all this raw video footage and I have no friggin' idea what to do with it. What am I supposed to do, have students graph the height of the ball vs. time and realize that there are some relationships that aren't linear?
My students are even getting into the taping. They look so cute and happy throwing the ball back and forth, but little do they know that one day this concept of math actually helping them to interpret the world around them can consume them. What's next? Are we going to start treating mathematics like a humanity and sit around discussing it as if it were a piece of literature or work or art? Don't you know that math is only supposed to be important 8:20-2:55 in Room 405 from September to June? Don't you know that math is supposed to be a set of rules that we force our kids to memorize until April 22 and then they aren't supposed to think about it again? Get with the program, will ya?
And no textbook? C'mon, man! What are you thinking? Those things were all written by people who really care about making math matter to our children. Don't you know that the more a student sits in front of a textbook, the more they learn? I saw some research done by an independent agency Houghton, McGraw, Holt and Littell that says students can actually teach themselves with these things.
In closing, you have got it all wrong. Kids want to have subjects forced upon them. They want to be told the rules, they want to mindlessly copy exactly what the teacher says and does and they especially want to ask questions like, "I don't get it."
Inquiry? Yeah, right!
Sincerely,
David
p.s. Can I make a cameo in Graphing Stories vol. 2?
p.p.s Can you all help me package this up into a series of lessons?
The Never Ending Question
Teacher: So what is the value of f(x) if x =3?
Student: Does f(x) mean f times x?
Teacher: No, no, no...f(x) is a function of x.
Student: Oh, it is a function of x?
Teacher: Right.
Student: Oh, okay, I think I get it. So we can plug in a number for x and find out what f equals.
Teacher: Yeah, that's pretty close. Do you have another question?
Student: So, then is f like the slope of the line?
Teacher: *slaps forehead* Uncle!
Student: Well you said it is a function of x and of means to multiply.
Alright, so that didn't just happen in my class. But similar dialogues do take place right around the time I first introduce things like f(x) or sin(x). Kids always think that means that we are multiplying something by x. We usually end up discussing how often times functions need to have names like f(x) or g(x) so you can tell them apart. We don't spend too much time on function notation in middle school, but when it comes up, I would like a better way to explain it.
Don't act like that hasn't happened to you.
So how do you explain it?
Student: Does f(x) mean f times x?
Teacher: No, no, no...f(x) is a function of x.
Student: Oh, it is a function of x?
Teacher: Right.
Student: Oh, okay, I think I get it. So we can plug in a number for x and find out what f equals.
Teacher: Yeah, that's pretty close. Do you have another question?
Student: So, then is f like the slope of the line?
Teacher: *slaps forehead* Uncle!
Student: Well you said it is a function of x and of means to multiply.
Alright, so that didn't just happen in my class. But similar dialogues do take place right around the time I first introduce things like f(x) or sin(x). Kids always think that means that we are multiplying something by x. We usually end up discussing how often times functions need to have names like f(x) or g(x) so you can tell them apart. We don't spend too much time on function notation in middle school, but when it comes up, I would like a better way to explain it.
Don't act like that hasn't happened to you.
So how do you explain it?
Wednesday, April 22, 2009
Sincerely, Markus Hohenwarter
Every day at 5:00 pm I receive an email from Markus Hohenwarter. It isn't a "hey how are you doing?" kind of email, this one is all business. Actually it isn't even a personal email, it is one of those mass emails that often ends up in the spam box. But more times than not, this spam is worth reading.
Markus Hohenwarter is the creator of GeoGebra which has to be one of my top three classroom tools. The email is generated by the Geogebra upload manager and lists all of the different GeoGebra files (both .html and .ggb) that have been uploaded to the bank during the previous day. Many of the dynamic .html worksheets are ready for classroom use and author attribution is at the bottom of the page. However, if you like the concept of the worksheet but would like to use your own questions, you can download the .ggb file and learn how the sheet was created by viewing the construction protocol.
The only downside to the upload manager is that the uploads aren't tagged, so you have to do bit of hunting to find someting worth while. Regardless, this is yet another reason to love GeoGebra!
Markus Hohenwarter is the creator of GeoGebra which has to be one of my top three classroom tools. The email is generated by the Geogebra upload manager and lists all of the different GeoGebra files (both .html and .ggb) that have been uploaded to the bank during the previous day. Many of the dynamic .html worksheets are ready for classroom use and author attribution is at the bottom of the page. However, if you like the concept of the worksheet but would like to use your own questions, you can download the .ggb file and learn how the sheet was created by viewing the construction protocol.
The only downside to the upload manager is that the uploads aren't tagged, so you have to do bit of hunting to find someting worth while. Regardless, this is yet another reason to love GeoGebra!
Tuesday, April 21, 2009
Bridging the Gap
This one goes out to all the algebra teachers; especially those in middle school. Anyone notice that kids "get it" in 7th grade and then act like they have never seen a variable once they hit algebra? Or am I the only one? We had nearly 70% of our 7th graders proficient and above on last year's CST's, but only 40% of our algebra students were proficient. If you take the advanced classes out of the mix, it is more like 60% to 30%. I know, I know, you can't base what a kid knows solely on a standardized test. But, those numbers are pretty indicative of how the kids actually do in class. Some will say that algebra is just too abstract for most 8th grade kids. I don't know if I buy that, especially when I read articles like this.
I am going to have some release time once testing is over in order to adjust our pacing guides and I would like to be able to develop some lesson ideas to help our teachers bridge the gap between number sense and algebraic thinking. Maybe some of you have already tackled this. I would love to hear what you have done. How have you sequenced your 7th grade curriculum and how have you helped move your students from numeric fluency to algebraic proficiency? I figure if I am going to lock myself in a room and try to hash this out, you may as well be there with me!
I am going to have some release time once testing is over in order to adjust our pacing guides and I would like to be able to develop some lesson ideas to help our teachers bridge the gap between number sense and algebraic thinking. Maybe some of you have already tackled this. I would love to hear what you have done. How have you sequenced your 7th grade curriculum and how have you helped move your students from numeric fluency to algebraic proficiency? I figure if I am going to lock myself in a room and try to hash this out, you may as well be there with me!
Can I Get In Trouble For This?
Testing started today. I have done everything within my power to make my classroom as non-mathy as possible. No work on the boards. All procedure posters covered. I even attempted to remove the letters A,B,C,D,F,G,H,J from any text on my walls. However, this one slipped by:

Uh oh! I am sure this is one of the answers to one of the problems. I hope the students don't see it.

Uh oh! I am sure this is one of the answers to one of the problems. I hope the students don't see it.
Wednesday, April 15, 2009
Confessions of a 13 Year Veteran
Ok, I admit it. My lesson planning skills suck! It just hit me the other day. I am reading all your blogs and seeing all the cool things you are doing in your classrooms, and all I can ask myself is, "Why don't I think of stuff like that?"
I think I know why. I cut my teeth on CPM (another post on CPM coming soon) and all of my lessons were pre packaged. All I needed to learn was to ask good questions and get out of the way. That suited my style very well. By the time NCLB came around and we dropped CPM, my school was already going lock step with pacing guides and common assessments. Neither one of these approaches allowed for much innovation nor did they require a bunch of thought. It didn't help that I became the varsity baseball coach in my first full year of teaching and spent way more time planning practice than I did lessons. The real problem was that I didn't really know how much I had bitten off until recently.
Now that I am teaching middle school math as the high school guy brought in to handle all the GATE kids, I am not only responsible for my own classes but for setting a tone and pace for an entire department. I feel more accountability now than ever before. It has been in these last three years that I have really started to ask reflective questions regarding not only my practice, but good practice in general. I also have access to tools that I didn't even know existed when I was at the high school.
So here is a snapshot of where my lessons were compared to where they are. Feel free to take your shots and help me make this better. This lesson is stolen borrowed adapted from a lesson in the April 2009 issue of Mathematics Teaching in the Middle School.
I don't know if I would have even bothered to re type the lesson, I may have just photo copied it and given it like this:

I would have passed out this handout and told the students to represent each savings plan as a: graph, input/output table, algebraic expression and verbal expression. My students would have muddled through it and most would have just jumped through another hoop.
I toggled between these four slides and asked students to pick out what information they thought was important. It was interesting that some students felt it necessary to try to copy the information while the rest of the class was willing to observe and jot down what they thought was essential info.
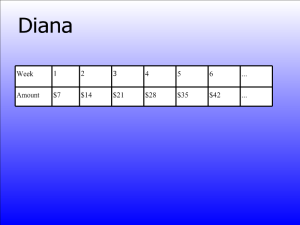
Questions students came up with:

Teacher: "What can you tell me about Yoni?"
Class: "She has $300."
Teacher: "How much will she have in 3 weeks? 2 years? 100 years?
Class: "$300. $300. $300."
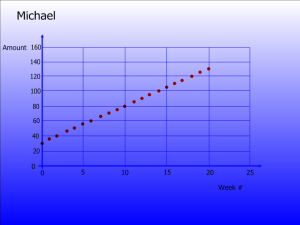
A few students were quick to point out that we only needed to focus on two or three key points in order to make a generalization of Michael's situation. They immediately zoomed in on (0, 30) and (10, 80). However, I did have one group who decided to focus on the last point (20, 130). They decided that Michael averaged $6.50 per week. But when they were asked if their trend would continue, they quickly realized that they had failed to consider the original amount of Michael's savings.
Chandler, one of my 7th graders decided to ask, "Does x represent weeks?" Beautiful, that info was on the next slide.
The question of the day had to come from Paul: "So, if the only point we know for sure in Michael's graph is (30, 80) wouldn't he have more money if he actually started at (0,0)? In his mind he was seeing this...
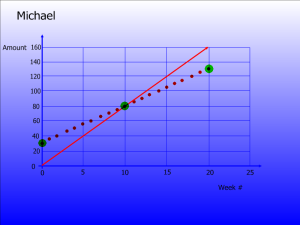
...which led to an interesting discussion on how slope represents the amount of money saved per week.
My students are starting to catch on to how things work in my class because as soon as these slides came up:


I asked, "What is my next question?" To which they all responded:

Once they had made the decision on which represenation they prefered, I had them represent the other three savings plans the same way.
At first the justifications for "why" one representation was preferred over another were weak at best, lazy and unthoughtful at worst:
Okay, that last one was mine, but you get the point. Being the father of four boys, I can smell an "alright get off my back, already" answer a mile away, I continued to prod. Eventually we had answers like this:
We eventually got to the discussion on "Who has the most money right now?"
Hands fly upright around the same time I hear: "Yoni! Danny!"
Then Adrian pipes up, "When is now?"
Gotta love that kid!
I think I know why. I cut my teeth on CPM (another post on CPM coming soon) and all of my lessons were pre packaged. All I needed to learn was to ask good questions and get out of the way. That suited my style very well. By the time NCLB came around and we dropped CPM, my school was already going lock step with pacing guides and common assessments. Neither one of these approaches allowed for much innovation nor did they require a bunch of thought. It didn't help that I became the varsity baseball coach in my first full year of teaching and spent way more time planning practice than I did lessons. The real problem was that I didn't really know how much I had bitten off until recently.
Now that I am teaching middle school math as the high school guy brought in to handle all the GATE kids, I am not only responsible for my own classes but for setting a tone and pace for an entire department. I feel more accountability now than ever before. It has been in these last three years that I have really started to ask reflective questions regarding not only my practice, but good practice in general. I also have access to tools that I didn't even know existed when I was at the high school.
So here is a snapshot of where my lessons were compared to where they are. Feel free to take your shots and help me make this better. This lesson is stolen borrowed adapted from a lesson in the April 2009 issue of Mathematics Teaching in the Middle School.
What I would have done before:
I don't know if I would have even bothered to re type the lesson, I may have just photo copied it and given it like this:

I would have passed out this handout and told the students to represent each savings plan as a: graph, input/output table, algebraic expression and verbal expression. My students would have muddled through it and most would have just jumped through another hoop.
What I did today:
I toggled between these four slides and asked students to pick out what information they thought was important. It was interesting that some students felt it necessary to try to copy the information while the rest of the class was willing to observe and jot down what they thought was essential info.

Questions students came up with:
- Does the chart represent the amount of money Diana makes each week or the total she has saved?
- Will she continue to save at this rate? "Yeah, look at the "dot, dot, dot."

Teacher: "What can you tell me about Yoni?"
Class: "She has $300."
Teacher: "How much will she have in 3 weeks? 2 years? 100 years?
Class: "$300. $300. $300."

A few students were quick to point out that we only needed to focus on two or three key points in order to make a generalization of Michael's situation. They immediately zoomed in on (0, 30) and (10, 80). However, I did have one group who decided to focus on the last point (20, 130). They decided that Michael averaged $6.50 per week. But when they were asked if their trend would continue, they quickly realized that they had failed to consider the original amount of Michael's savings.

Chandler, one of my 7th graders decided to ask, "Does x represent weeks?" Beautiful, that info was on the next slide.
The question of the day had to come from Paul: "So, if the only point we know for sure in Michael's graph is (30, 80) wouldn't he have more money if he actually started at (0,0)? In his mind he was seeing this...

...which led to an interesting discussion on how slope represents the amount of money saved per week.
My students are starting to catch on to how things work in my class because as soon as these slides came up:



I asked, "What is my next question?" To which they all responded:

Once they had made the decision on which represenation they prefered, I had them represent the other three savings plans the same way.
At first the justifications for "why" one representation was preferred over another were weak at best, lazy and unthoughtful at worst:
- An input/output table is more organized.
- It's easier to see the data.
- I like it better because it is better and less worse than the others.
Okay, that last one was mine, but you get the point. Being the father of four boys, I can smell an "alright get off my back, already" answer a mile away, I continued to prod. Eventually we had answers like this:
- I prefer the chart because it is easier to see which numbers go together; on the graph, you have to work a little more to see which numbers are related.
- I prefer the graph because I can actually see how the different points relate. The slope helps me see how fast someone is saving.
- I prefer the verbal expression because it helps me understand the overall situation better.
We eventually got to the discussion on "Who has the most money right now?"
Hands fly upright around the same time I hear: "Yoni! Danny!"
Then Adrian pipes up, "When is now?"
Gotta love that kid!
Subscribe to:
Posts (Atom)








