Are Two Ways Better Than One?

Graphing parabolas is much easier when we can zero in on "key points."  The CPM Algebra 2 curriculum was great about dealing with "parent graphs" and then showing students the process for translating and stretching these parents.  It is easy to get away from this as we have other skills that we need to teach.  But this year, I have really focused on having my students get really comfortable with y = x² and then recognizing that all parabolas are really just different perspectives of this parent graph.  Zoom out and the parabola get skinnier; zoom in and it gets fatter.  If you know the vertex and stretch factor, then you are ready to do some graphing;  this works for vertex or standard form.

One of the more interesting developments during this unit has been my students recognizing that the rate of change in a parabola has a rate of change.  They are wrestling with the concepts behind derivatives and I want to keep them in that fight as long as possible.  I usually have my students graph five points and I have always had them relate those five points back to the vertex.  However, with the way they are handling rate of change, I need to rethink my process. 

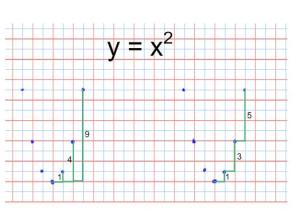
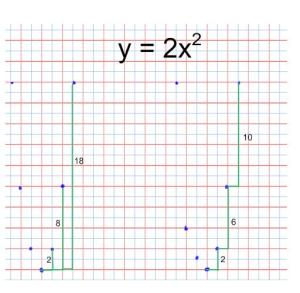
Simply use the stretch factor to adjust the relationships: This year I have given them choice on this, but it has caused a few kids confusion as they end up with a hybrid process.  Next year? Not so sure.