Question: How can we find the diagonal length of any rectangle?
Part 1: On a sheet of paper, draw the following rectangles:
A. 3 x 4
B. 5 x 12
C. 6 x 8
D. 8 x 15
Part 2: Draw the diagonal for each rectangle.
Part 3: Measure the length of each diagonal and record it in the table below.
| Rectangle | Side 1 | Side 2 | Diagonal |
| A | 3 | 4 | 5 |
| B | 5 | 12 | |
| C | 6 | 8 | |
| D | 8 | 15 |
Part 4: Use the side lengths of the rectangle, addition, multiplication and square root to write an expression that equals the diagonal length.
Rectangle 1 would look like this:
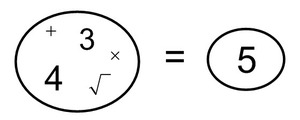
Be sure that your equation works for each of the rectangles.
Part 5: Write a general equation that could be used for any rectangle.
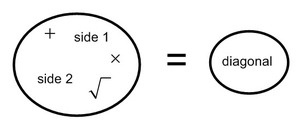
Part 6: Draw a new a x b rectangle. Use your equation from part 5 to predict what the diagonal length should be.
Part 7: How accurate was your prediction? Explain.
Commentary
This task asks students to notice a special relationship between the sides of rectangle and its diagonal, which they can later apply to the sides of a right triangle and its hypotenuse. It is the numeric counterpart to task Sizing Up Squares, which looks at the same relationship geometrically. Students will draw rectangles of given side lengths, measure the diagonals, and then find an equation that relate the sides to the diagonal using specified operations: addition, multiplication, and square roots. Once students have an equation that works for the initial data, they will write a general equation, and test this hypothesis against other rectangles of their choosing.
This task allows students to construct right triangles indirectly (in the context of rectangles and diagonals), observe the relationship between their side lengths, and then "play" with the numbers and use inductive reasoning to discover the Pythagorean relationship.
Teacher Note: (1) Units are not specified here so there is flexibility in how students construct the rectangles. If graph paper is used, students may need guidance with regard to measuring the diagonal lengths. For example: if using the unit of the graph paper to construct the sides of the rectangles but using a ruler to measure the diagonals, they will need to divide the ruler measurements by the size of the grid to ensure that the numbers being compared are in the same unit. Alternatively, they could use a strip of the same graph paper as the "ruler," with the unit of measurement being the side length of each square on the paper. (2) Use of calculators may facilitate students' experimentation with the numbers in Part 4.





3 comments:
I know the formula, but am having a hard time imagining students figuring out to square the legs and add them and then take the square root. This process would not be obvious to me without my background knowledge. How do we help students make this jump?
And even if they do manage to combine operations in just the right way, is it a problem that it just ... seems to work? Where does deduction and proof figure in here?
This task is part of a larger project. I have a unit writer that requested a very specific task and deduction/proof will come in other tasks. This particular task didn't meet the specs for Illustrative Mathematics so, as a workaround, we posted here.
Post a Comment